Una curva paramétrica en el plano puede entenderse informalmente con la «estela» que deja un punto en movimiento. Formalmente, una curva paramétrica en el plano es una función continua \(\textbf{u}:I \to \mathbb{R} ^2\) donde \(I\) es un intervalo de \(\mathbb{R}\).
Interpretamos entonces que \(I\) es un intervalo de tiempo y que para cada \(t \in I\), el punto se sitúa en la posición \(\textbf{u}(t)=(x(t), y(t))\).
En este caso, la continuidad de la función \(\textbf{u}\) equivale a la continuidad de las funciones coordenadas \(x(t)\) e \(y(t)\).

Primeros ejemplos: la circunferencia

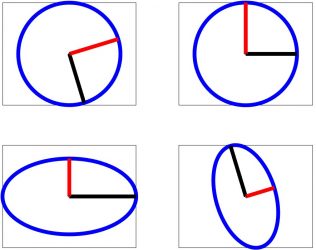
La curva \(\textbf{u}(t)=(\cos t, \sin t),\, t \in [0,2\pi]\) recorre la circunferencia unidad \(x^2+y^2=1\) en sentido antihorario. Por otra parte, la curva \(\textbf{u}(t)=(\cos t, – \sin t), t \in [0,2\pi]\) recorre la circunferencia unidad en sentido horario. La curva \(\textbf{u}(t)=(\cos t, \sin t), t \in [0,4\pi]\) recorre dos veces la circunferencia unidad.

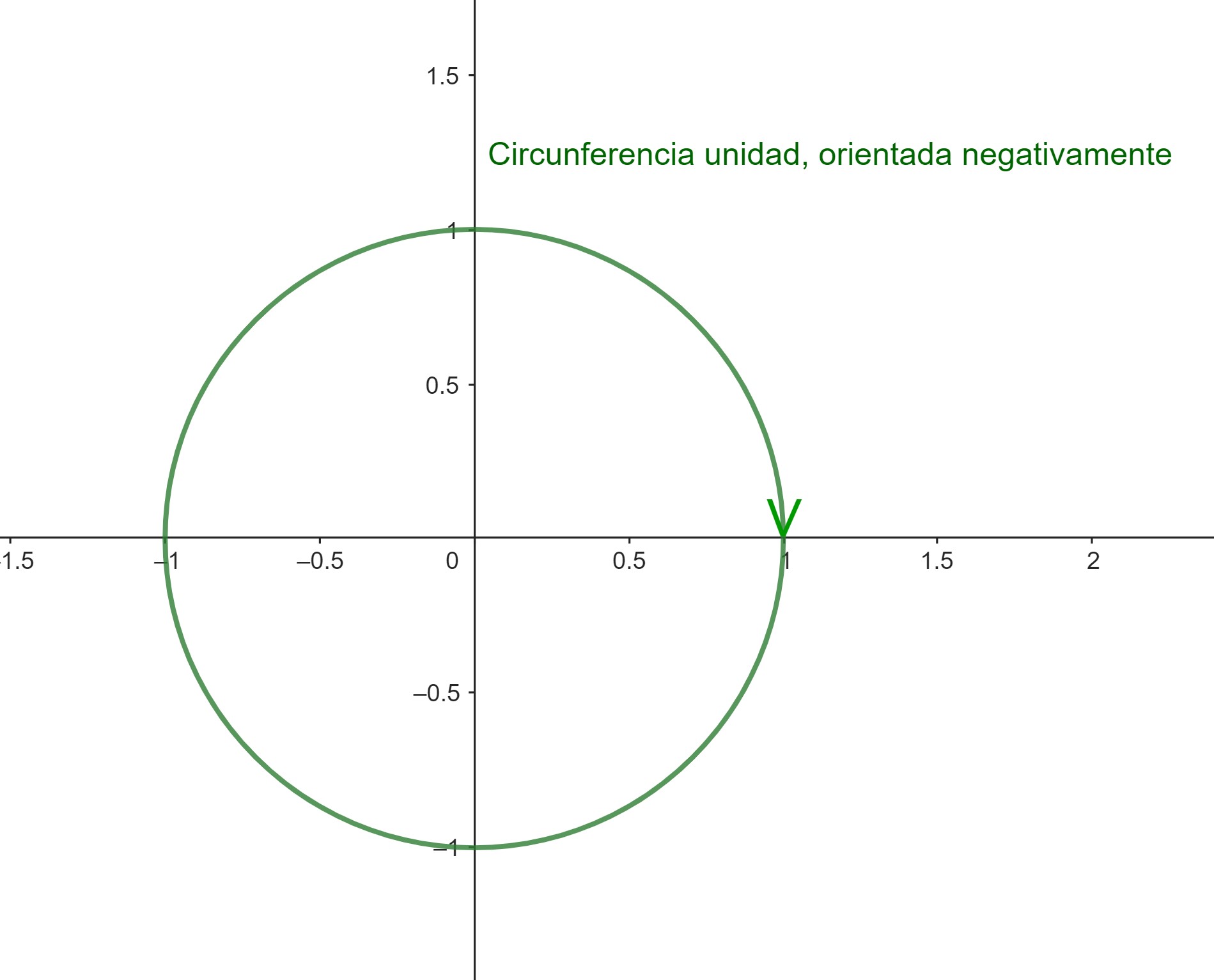Conviene distinguir entre la curva paramétrica, que es una aplicación \(\textbf{u}:I \to \mathbb{R} ^2\), y la imagen de la curva, que es el conjunto de puntos en el plano
\({\textbf{u}(t): t \in I}\). En general, el intervalo \(I\) puede ser abierto o cerrado, acotado o no.

En los tres ejemplos anteriores, la imagen de la curva es la misma, aunque se trata de curvas diferentes.

Curvas explícitas: Si \(f: I \to \mathbb{R}\) es una función continua, su gráfica es la imagen de una curva paramétrica, definida por \(\textbf{u}(t)=(t,f(t))\), \(t \in I\).

Una recta como curva paramétrica

Si pensamos en una trayectoria rectilínea, toda recta en el plano es una curva paramétrica. En concreto, si \(P\) es un punto de la recta y \(\textbf{v}\) es un vector director, la recta paramétrica tiene como ecuación

$$
\textbf{u}(t)=P+t \textbf{v} \, , \, t \in\mathbb{R} \, .
$$

Otro ejemplo clásico: la elipse

La curva \(\textbf{u}(t)=(2\cos t, 3\sin t),\, t \in [0,2\pi]\) recorre la elipse \(x^2/4+y^2/9=1\), en sentido antihorario, comenzando en el instante \(t=0\) en el punto \((2,0)\). De manera análoga, curva \(\textbf{u}(t)=(-2\cos t, 3\sin t),\, t \in [0,2\pi]\) recorre la elipse \(x^2/4+y^2/9=1\) en sentido horario, comenzando para \(t=0\) en el punto \( (-2,0) \).

Más ejemplos clásicos: la espiral

La espiral de Arquímedes, definida por \(\textbf{u}(t)=(t \cos t, t \sin t) , \, t\in [0,+\infty)\) gira alrededor del origen en sentido antihorario. La intersección de la imagen de la curva con el semieje positivo de abscisas se produce en los puntos \((2 n \pi, 0)\), que están equiespaciados.

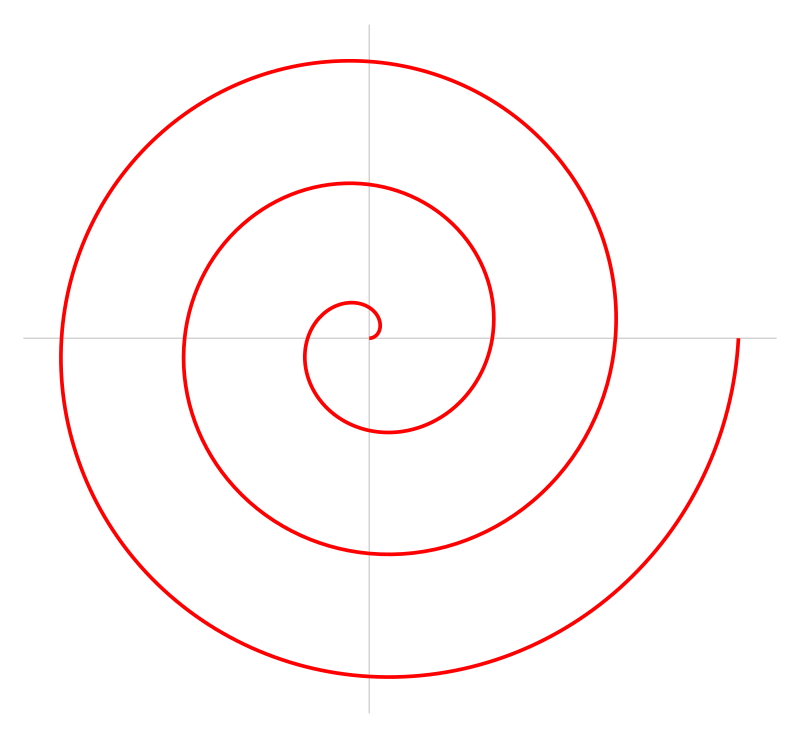
Este tipo de espiral equiespaciada se utilizaba en los surcos de los discos de vinilo.

Toda curva es una función continua aunque, en general, no tiene por qué ser derivable. La derivabilidad de la curva \(\textbf{u}(t)=(x(t), y(t))\) en el instante \(t_0 \in I\) es equivalente a la derivabilidad de sus dos coordenadas, \(x(t)\) e \(y(t)\), en \(t_0\). En este caso, se define el vector velocidad como \(\textbf{v}(t_0)=\textbf{u}'(t_0)=(x'(t_0), y'(t_0))\), es decir,

$$
\textbf{v}(t_0)= \textbf{u}'(t_0)= \lim_{t \to t_0}\frac{1}{t-t_0}(\textbf{u}(t)-\textbf{u}(t_0))
$$

Si el vector \(\textbf{u}'(t_0)=(x'(t_0), y'(t_0))\) es distinto de \((0,0)\), representa un vector tangente a la curva en el instante \(t_0\), que se obtiene como límite de los vectores secantes a la curva \(\frac{1}{t-t_0}(\textbf{u}(t)-\textbf{u}(t_0))\). La recta tangente a la curva en el instante \(t_0\) tiene como ecuación paramétrica \(\textbf{r}(t)=\textbf{u}(t_0)+t \textbf{v}(t_0)\).

Primeros ejemplos: la circunferencia y la elipse

Si consideramos la curva \(\textbf{u}(t)=(\cos t, \sin t),\, t \in [0,2\pi]\), el vector tangente en el instante \(t_0\) es \((-\sin t_0, \cos t_0)\). La recta tangente en \(\textbf{u}(t_0)\) es

$$
\textbf{r}(t)=
(\cos t_0-t \sin t_0, \sin t_0+ t \cos t_0)
$$

En el caso de la elipse \(\textbf{u}(t)=(2\cos t, 3\sin t),\, t \in [0,2\pi]\), la recta tangente en el punto \((0,-3)\) correspondiente al valor del parámetro \(t=3\pi/2\), es la recta \(y=-3\).

Otro ejemplo clásico: la lemniscata

La lemniscata de Gerono es una curva que pasa por el origen en instantes diferentes con inclinaciones distintas. En concreto, las ecuaciones paramétricas son \(\textbf{u}(t)=(\cos t, \cos t \sin t)\). Para \(t_0=\pi /2\) y \(t_1=3\pi / 2\), tenemos que \(\textbf{u}(t_0)=\textbf{u}(t_1)=(0,0)\), mientras que \(\textbf{u}'(t_0)=(-1,-1)\) y \(\textbf{u}'(t_1)=(1,-1)\).

La ecuación de la lemniscata de Gerono en forma implícita es \(x^4-x^2+y^2=0\). Para distintos valores del parámetro \(d>0\) la ecuacíon \((x^2+y^2)^2=2 d(x^2-y^2)\) describe una curva denominada lemniscata de Bernoulli. Se trata de la formada por aquellos puntos \(P\) del plano que cumplen que, dados dos focos \(F_1\) y \(F_2\) a distancia \(d\), el producto de las distancias de \(P\) a los focos es \(d^2\).

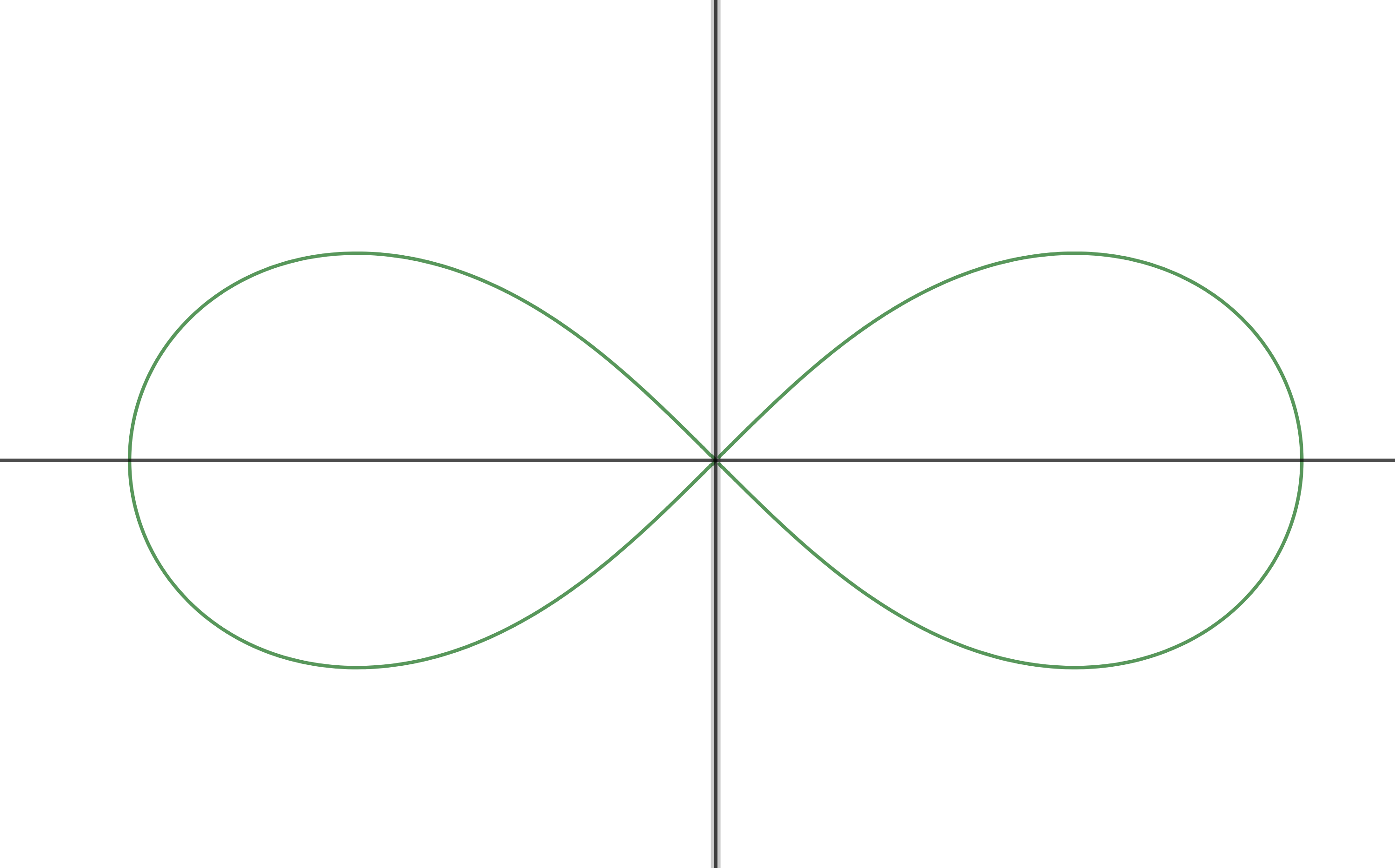Se puede encontrar más información sobre la lemniscata (y sus variantes) en el siguiente enlace de Wikipedia.

Una curva mecánica: la cicloide

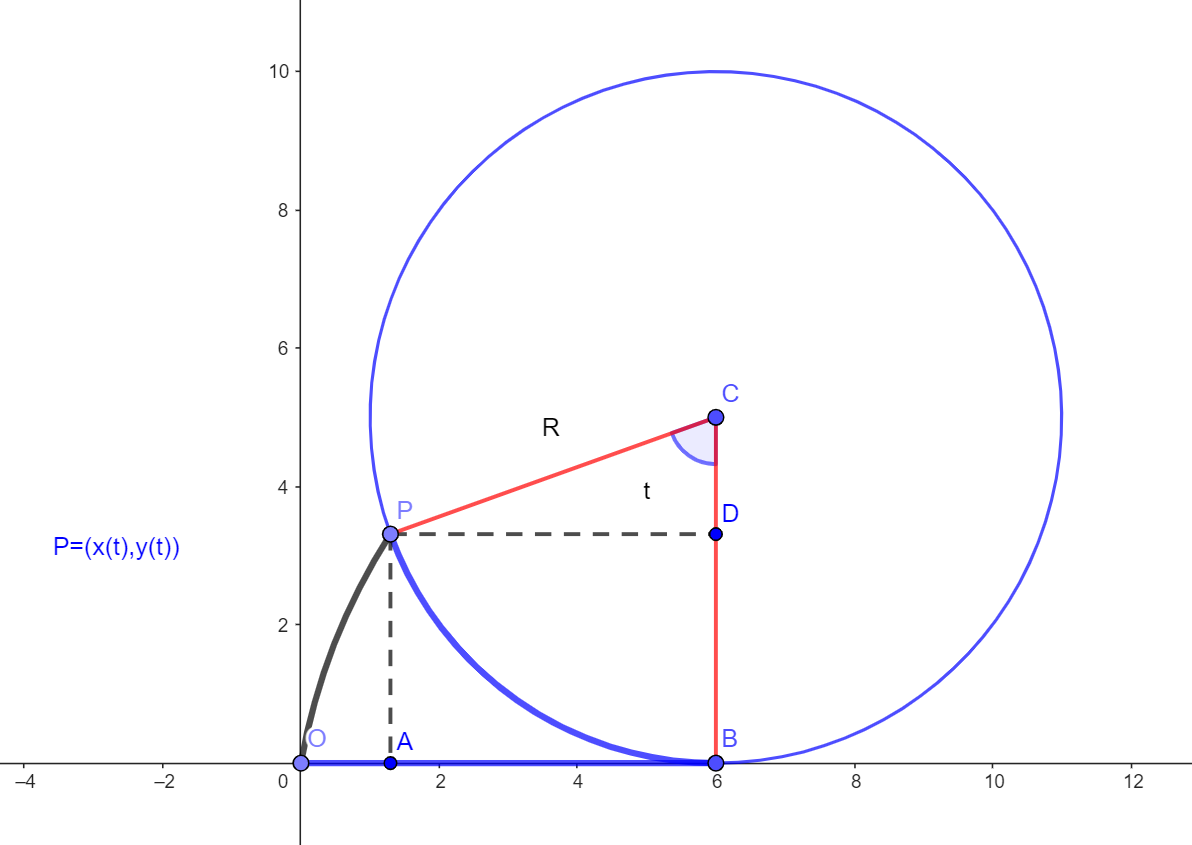
Otra curva clásica es la cicloide, que se define como la curva que describe un punto fijo de una circunferencia de radio $R$ que rueda sin deslizamiento sobre el eje de abscisas.

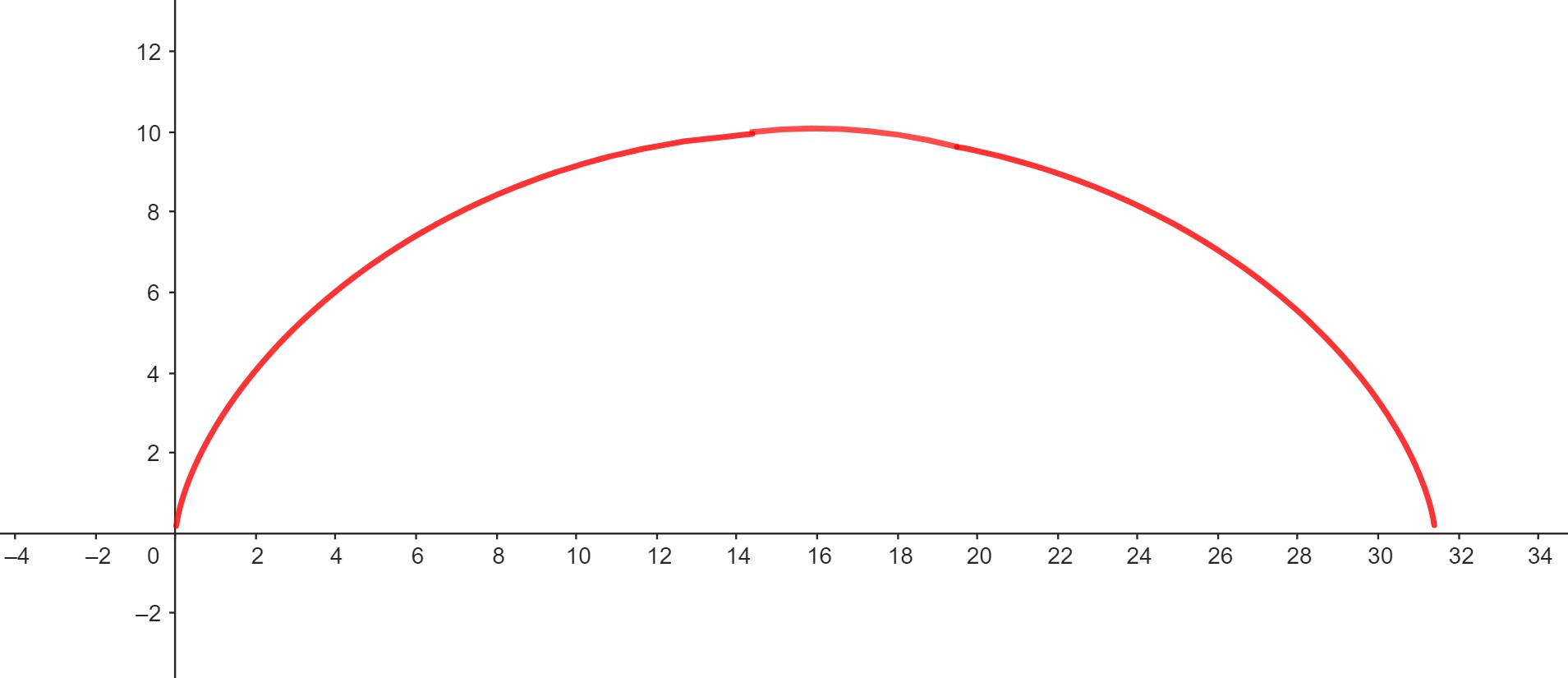Para obtener las ecuaciones de la cicloide, consideramos el movimiento del punto \(P=(0,0)\), que el eje de ordenadas coincide con el diámetro de la circunferencia. En este caso, de acuerdo con la figura, vemos que la distancia \(OB\) coincide con la longitud de arco \(PB\). Si \(t\) es el ángulo que se indica en la figura, se deduce que

$$
\left\{
\begin{array}{l}
x(t)=\overline{OB}-\overline{AB}= R t – R \sin t \
y(t)=\overline{CB}-\overline{CD}= R – R \cos t
\end{array}
\right\}.
$$

Curvas paramétricas continuas frente a curvas derivables

Un ejemplo típico de función continua que no es derivable en \(t=0\) es la función \(f(t)=|t|\). Esto refleja que la gráfica de la función \(f\) «tiene un pico»» en \((0,0)\).
Por tanto, la curva paramétrica \((t,|t|)\) no tiene un vector tangente definido en \(t=0\).
Sin embargo, la imagen de esta curva admite una parametrización derivable en todos los puntos. Para pasar con diferenciabilidad por el pico de la gráfica será necesario que el vector velocidad se anule. Es decir, que el movimiento se detenga en ese punto. En concreto, la curva
\(\textbf{u}(t)=(t^3, t^2 |t|)\) es derivable en todo \(t\), \(\textbf{u}'(0)=(0,0)\) y la imagen de \(\textbf{u}(t)\) es la gráfica de \(y=|x|\) en \(\mathbb{R}^2\).

Es posible construir ejemplos de funciones continuas que no son derivables en ningún punto, como la familia de funciones de Weierstrass \(f(t)=\sum_{n=0}^{\infty}a^n \cos(b^n \pi t)\), con \(a,b\) apropiados. Se pueden consultar más detalles en el artículo de Wikipedia dedicado a la Función de Weierstrass. Esto muestra que hay funciones continuas que presentan comportamientos patológicos. En este sentido, se puede demostrar que existen curvas paramétricas continuas cuya imagen llena todo un cuadrado.
Sobre este tipo de fenómenos, se puede consultar el artículo de Wikipedia dedicado a la Curva de Peano o una de sus variantes, la Curva de Hilbert.

Las coordenadas polares en el plano vienen dadas por

$$
\left\{
\begin{array}{l}
x= r \cos \theta \\
y=r \sin \theta \end{array}\right.
$$

Es decir, se describe el punto \(P\) de coordenadas cartesianas \(P=(x,y)\) mediante el par \((r,\theta)\), donde \(r\geq 0\) mide la distancia de \(P\) al origen de coordenadas \(O\) y \(\theta\) es el ángulo que forman el semieje positivo de abscisas con la semirrecta \(OP\).

Algunas curvas admiten una parametrización utilizando las coordenadas polares cuando la curva viene dada por una relación \(r=f(\theta), \, \theta \in J\). En este caso, una parametrización de la curva es

$$
\textbf{u}(\theta)= ( f(\theta) \cos \theta,
f(\theta) \sin \theta), \, \, \theta \in J .
$$

Primer ejemplo: la circunferencia unidad

La curva \(\textbf{u}(\theta)=(\cos \theta, \sin \theta),\, \theta \in [0,2\pi]\) recorre la circunferencia unidad \(x^2+y^2=1\) en sentido antihorario. Se corresponde con la función \(f(\theta)=1\), por lo que \(r \equiv 1\).

Otro ejemplo de circunferencia

Analizamos la curva en polares \(r=2 \cos \theta\). Puesto que \(r\geq 0\), la curva solo existe para los valores de \(\theta\) para los que \(\cos \theta \geq 0\). Consideramos que \(\theta \in [-\pi/2, \pi/2]\). La curva admite la parametrización \(\textbf{u}(\theta)=(2 \cos^2 \theta, 2 \cos \theta \sin \theta)\). Para visualizar la curva, acudimos a las coordenadas cartesianas. Teniendo en cuenta que \(x=r \cos \theta\), la ecuación \(r=2 \cos \theta\) da lugar a \(r=2x/r\). Multiplicando por \(r\), como \(x^2+y^2=r^2\), se obtiene

$$
x^2+y^2=2x
$$

o, equivalentemente, \((x-1)^2+y^2=1\), que es la circunferencia de centro \((1,0)\) y radio \(1\).

Una curva clásica: la cardioide

La cardioide es una curva que se expresa en coordenadas polares como \(r= 1 + \cos (\theta)\). Esbozamos su gráfica. Es de ayuda dar distintos valores al ángulo \(\theta\) y calcular el radio correspondiente, observando las simetrías de la cardioide.

La ecuación de la cardioide en forma implícita es \((x^2+y^2-x)^2=x^2+y^2\).

Una variante de la espiral

La relación \(r=ab^{\theta}\), para \(a,b>0\), da lugar a una curva paramétrica conocida como «espiral logarítmica», ya que puede expresarse como \(\theta = \ln_b(r/a)\). Se trata de una curva, en la que los dos parámetros, \(a\) y \(b\), indican, respectivamente el tamaño de la espiral y, según \(b\) sea mayor o menor que \(1\), si esta se expande o se contrae.

Este tipo de espiral logarítmica aparece en multitud de situaciones en la naturaleza: a gran escala, en los brazos de las galaxias espirales (en particular, de la Vía Lactea), en los brazos de los ciclones o en geotecnia, en las fallas. En Biología también encontramos dicha curva: en telas de araña, en las conchas de molusco o en la trayectoria en que ciertos depredores se aproximas a sus presas.

Se puede encontrar más información sobre la espiral en el siguiente enlace de Wikipedia: Espiral – Wikipedia, la enciclopedia libre

Ejercicio:

Analizar la curva descrita en coordenadas polares por la expresión \(r=\cos(3 \theta)\), que es llamada «rosa de tres pétalos».

De manera análoga al caso bidimensional, se define una curva paramétrica en \(\mathbb{R}^n\) como una función continua \(\textbf{u}:I \to \mathbb{R}^n\), donde \(I\) es un intervalo de \(\mathbb{R}\). En este caso, para cada \(t \in I\), tenemos que \(\textbf{u}(t)=(x_1(t),x_2(t),\dots, x_n(t)) \in \mathbb{R}^n\). Las funciones \(x_j(t)\) son las coordenadas de \(\textbf{u}(t)\).

Una curva en \(\mathbb R^3\): la hélice

La hélice \(\textbf{u}(t)=(\cos t, \sin t , t),\, t\in\mathbb{R}\) es una curva en \(\mathbb R^3\), contenida en el cilindro \(x^2+y^2=1\). A medida que el tiempo \(t\) crece, la curva va rodeando el cilindro al tiempo que va ganando altura.

Se puede encontrar una hélice en la barandilla de una escalera de caracol. Y una doble hélice en la estructura física de una molécula de ADN.

Una curva \(\textbf{u}: I \to \mathbb R^n\) es derivable en \(t_0 \in I\) si lo son cada una de sus coordenadas \(x_j\), siendo

$$
\textbf{u}'(t_0)=(x_1′(t_0),x_2′(t_0),\dots, x_n'(t_0))
$$

Si, además, \(\textbf{u}'(t_0)\neq (0,0,\dots,0)\), la recta tangente a la curva en el instante \(t_0\) tiene como ecuación paramétrica \(\textbf{r}(t)=\textbf{u}(t_0)+t \textbf{u}'(t_0)\).

La recta tangente a la hélice \((\cos t, \sin t , t)\) en el instante \(t_0=\pi\) es

$$
\textbf{r}(t)=(-1, -t,\pi+t)
$$

La página de Math Insight contiene valiosa información, con muchas páginas interactivas sobre distintos temas. Además de tratar el tema de las curvas paramétricas, incluye multitud de ejemplos relativos funciones de varias variables, con distintos niveles de dificultad, para personas interesadas con diferentes niveles previos de preparación o interés. https://mathinsight.org/