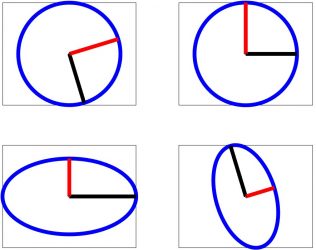
Imagen de una Circunferencia por una Aplicación Lineal

Motivación

Motivados por el estudio de los sistemas de Ecuaciones Diferenciales Ordinarias lineales de coeficientes constantes del tipo:

$$
\begin{pmatrix}
x'(t)\\
y'(t)
\end{pmatrix} = \begin{pmatrix}
a & b\\
c & d
\end{pmatrix} \cdot \begin{pmatrix}
x(t)\\
y(t)
\end{pmatrix}
$$

y más concretamente por la representación de las órbitas de sus soluciones en el denominado plano de fases, nos planteamos cómo calcular de un modo sencillo la imagen de una circunferencia por una aplicación lineal invertible.

Sea $P$ una matriz invertible $2\times 2$ que representa a una aplicación lineal de $\mathbb R^2$ en $\mathbb R^2$, y sea $S^1=\{(x,y): x^2+y^2=1\}$, la circunferencia unidad. Nos preguntamos, ¿quién es $P(S^1)$?

En primer lugar, notemos que la continuidad de $P$ nos asegura que nuestro conjunto será una curva cerrada por ser imagen de una curva cerrada (de hecho homeomorfa a $S^1$), mientras que la linealidad de $P$ nos dice que dicha curva será una cónica simétrica respecto al origen por ser la imagen de una cónica simétrica y centrada en el origen. De este modo, si denotamos por $E=P(S^1)$, nuestro objetivo es determinar una elipse $E$ centrada en el origen. Para ello, vamos a calcular sus dos ejes (aunque bastaría con uno de ellos porque ambos son ortogonales) y la longitud de los correspondientes semiejes.
Notemos que $E$ podría ser también una circunferencia, es decir, una elipse con los semiejes de la misma longitud.

Para resolver nuestro problema vamos a emplear dos métodos, uno algebraico (utilizando Álgebra de Matrices) y otro analítico (utilizando los Multiplicadores de Lagrange). Nos parece interesante exponer los dos, para hacer visible cómo diferentes puntos de vista resuelven una misma cuestión.

Método algebraico

Denotando los vectores de $\mathbb R^2$ por matrices columna y utilizando el lenguaje matricial, tenemos que

$$
(x,y)\in S^1 \Leftrightarrow \begin{pmatrix}
x\\
y
\end{pmatrix}^t \cdot \begin{pmatrix}
x\\
y
\end{pmatrix}=1,
$$

donde $t$ denota la matriz traspuesta.

Como $(\bar{x}, \bar{y})\in E$ si, y solo si, $P^{-1} (\bar{x}, \bar{y}) \in S^1$, donde $P^{-1}$ es la matriz inversa de $P$, tenemos que

$$
(\bar{x}, \bar{y})\in E \Leftrightarrow \Big( P^{-1} \cdot \begin{pmatrix}
\bar{x}\\
\bar{y}
\end{pmatrix} \Big)^t \cdot P^{-1} \cdot \begin{pmatrix}
\bar{x}\\
\bar{y}
\end{pmatrix} =1.
$$

O lo que es equivalente,

$$
(\bar{x}, \bar{y})\in E \Leftrightarrow \begin{pmatrix}
\bar{x}\\
\bar{y}
\end{pmatrix} ^t \cdot (P^{-1})^t\cdot P^{-1} \cdot \begin{pmatrix}
\bar{x}\\
\bar{y}
\end{pmatrix} =1.
$$

En consecuencia, la matriz simétrica $(P^{-1})^t\cdot P^{-1}$ es la matriz que nos da la ecuación de la elipse $E$. Para determinar sus ejes vamos a buscar la ecuación reducida de $E$, para lo cual vamos a realizar lo que se conoce como diagonalización por semejanza ortogonal de una matriz simétrica (véase Merino-Santos pag. 216).

Esto último quiere decir que existe una base ortonormal $\{\vec{v_1}, \vec{v_2}\}$ en $\mathbb R^2$ tal que

$$
(P^{-1})^t\cdot P^{-1}= Q\cdot D \cdot Q^{-1}
$$

donde:

$D$ es una matriz diagonal conteniendo los autovalores $\alpha$ y $\beta$ de la matriz $(P^{-1})^t\cdot P^{-1}$ (que son reales y no nulos por ser simétrica e invertible),
$Q$ es una matriz ortogonal (i.e. $Q^{-1}= Q^t$) que tiene por columnas los autovectores correspondientes, i.e., $Q=(\vec{v_1} | \vec{v_2})$.

Es fácil comprobar que $(P^{-1})^t\cdot P^{-1}$ es además definida positiva por lo que sus autovalores deben ser positivos.

En consecuencia, la ecuación de $E$ queda:

$$
\begin{pmatrix}
\bar{x}\\
\bar{y}
\end{pmatrix} ^t \cdot Q\cdot D \cdot Q^t \begin{pmatrix}
\bar{x}\\
\bar{y}
\end{pmatrix} =1
$$

Es decir,

$$
\Big ( Q^t \cdot \begin{pmatrix}
\bar{x}\\
\bar{y}
\end{pmatrix}\Big ) ^t \cdot \begin{pmatrix}
\alpha & 0\\
0 & \beta
\end{pmatrix} \cdot Q^t \begin{pmatrix}
\bar{x}\\
\bar{y}
\end{pmatrix} =1
$$

Lo que nos dice la igualdad anterior es que el cambio de variables que debemos hacer para llegar a la ecuación reducida de la elipse es el que da la matriz $Q^t$, o lo que es lo mismo $Q^{-1}$.

Notemos que la transformación dada por $Q=(\vec{v_1} | \vec{v_2})$ lleva la base canónica de $\mathbb R^2$ a la base $\{\vec{v_1}, \vec{v_2}\}$, por lo que $Q^{-1}$ llevará esta base a la canónica. Es decir, la aplicación $Q^{-1}$ coloca los ejes de la elipse sobre los ejes coordenados.

Esto significa que la ecuación de la elipse en las nuevas coordenadas $(x’, y’)= Q^{-1}(\bar{x}, \bar{y})$ será $\alpha (x’)^2 +\beta (y’)^2=1$, o equivalentemente

$$
\frac{(x’)^2}{(\sqrt{1/\alpha})^2} + \frac{(y’)^2}{(\sqrt{1/\beta})^2 } = 1.
$$

Por lo que deducimos que las longitudes de los semiejes serán la raíz cuadrada de $1/\alpha$ y de $1/\beta$, respectivamente.

En definitiva, ya hemos resuelto el problema inicial.

Los ejes de $E$ están situados en las rectas generadas por los autovectores $\vec{v_1}$ y $\vec{v_2}$, y las longitudes de los semiejes serán la raíz cuadrada de los inversos de los correspondientes autovalores, todo ello referido a la matriz $(P^{-1})^t\cdot P^{-1}$.

A continuación, vamos a ver cómo es posible obtener todos estos datos directamente a través de la matriz inicial $P$. En efecto, sean:

$\vec{u_1}$ y $\vec{u_2}$ tales que $P(\vec{u_1})=\vec{v_1}$ y
$P(\vec{u_2})=\vec{v_2}$.

Como $(P^{-1})^t\cdot P^{-1}(\vec{v_1})=\alpha \vec{v_1}$, entonces $(P^{-1})^t\cdot P^{-1}(P(\vec{u_1}))=\alpha P(\vec{u_1})$, luego $(P^{-1})^t(\vec{u_1})=\alpha P(\vec{u_1})$. Es decir, $\vec{u_1}=\alpha P^t\cdot P(\vec{u_1})$, de lo que deducimos que $\vec{u_1}$ y análogamente $\vec{u_2}$ son autovectores de la matriz $P^t\cdot P$ correspondientes a los autovalores $1/\alpha$ y $1/\beta$, respectivamente.

De todo lo anterior deducimos que la elipse $E=P(S^1)$ queda determinada haciendo lo siguiente:

Calculamos los autovalores $\lambda_1$ y $\lambda_2$ de $P^t\cdot P$.
Tomamos una base de autovectores $\{\vec{u_1}, \vec{u_2}\}$ de $P^t\cdot P$ asociados a dichos autovalores.
Los ejes de $E$ están sobre las rectas generadas por $P(\vec{u_1})$ y $P(\vec{u_2})$, respectivamente.
Las longitudes de los semiejes son $\sqrt{\lambda_1}$ y $\sqrt{\lambda_2}$.

Notemos que si $\lambda_1=\lambda_2$ entonces $E$ es la circunferencia de centro el origen y radio $\sqrt{\lambda_1}$.

Por otro lado, los puntos 2) y 3) pueden simplificarse teniendo en cuenta que los ejes de $E$ son ortogonales,
de modo que bastaría con calcular un único autovector.

En Álgebra Lineal Numérica se definen los valores singulares de una matriz $P$ como las raíces cuadradas de los autovalores (no negativos) de la matriz $P^t\cdot P$.
En consecuencia, las longitudes de los semiejes de la elipse $P(S^1)$ no son más que los valores singulares de la matriz $P$.

Método analítico

Otro modo de determinar la elipse $E=P(S^1)$ es a partir de los cuatro puntos que definen los dos ejes. Teniendo en cuenta que el eje mayor es el que pasa por los dos puntos (simétricos) más alejados del origen, es decir los de mayor norma, siendo esta norma la longitud del correspondiente semieje; y el eje menor es el que pasa por los dos puntos (simétricos) de menor norma, que será la longitud del semieje menor, tendremos que nuestro problema se traduce en calcular el máximo y el mínimo de la función norma euclídea o equivalentemente del cuadrado de la misma, restringida a los puntos de la elipse.

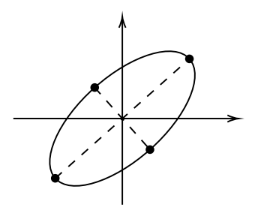
Se trata pues de un problema de máximos y mínimos de una función de dos variables sujeta a una restricción.

Más precisamente, queremos calcular los máximos y los mínimos de:

$$
f(x,y)=\|P(x,y)\|^2
$$

sujetos a la condición $g(x,y)=x^2+y^2-1=0$.

Planteamos este problema utilizando los denominados multiplicadores de Lagrange. Denotando por $\nabla$ el gradiente de una función y siendo $\lambda$ los multiplicadores de Lagrange, tenemos:

$$
\nabla f (x,y)=\lambda \cdot \nabla g (x,y)
$$

$$
x^2+y^2=1
$$

Es claro que $\nabla g (x,y) = 2 (x, y)$. Por otro lado, teniendo en cuenta que $f(x,y)= (\varphi\circ P)(x,y)$, donde $\varphi(u,v)=\|(u,v)\|^2=u^2+v^2$, y aplicando la regla de la cadena, tenemos:

$$
\nabla f (x, y)= \nabla \varphi(P(x,y)) \cdot D P(x, y)
$$

siendo $ D P(x, y)$ la diferencial de $P$ en el punto $(x,y)$. Como $P$ es una aplicación lineal entonces $ D P(x, y) = P$, para todo $(x,y)$. Además, $\nabla \varphi(u,v) = 2(u,v)$, por lo que se tiene:

$$
\nabla f (x, y)= 2 P(x,y) \cdot P = 2 \Big( P \cdot \begin{pmatrix}
x\\
y
\end{pmatrix} \Big)^t\cdot P
$$

En resumen, la igualdad $\nabla f (x,y)=\lambda \cdot \nabla g (x,y)$, nos quedará:

$$
\Big( P \cdot \begin{pmatrix}
x\\
y
\end{pmatrix} \Big)^t\cdot P = \lambda (x,y)
$$

o lo que es equivalente, tomando traspuesta,

$$
P^t\cdot P\begin{pmatrix}
x\\
y
\end{pmatrix} = \lambda \begin{pmatrix}
x\\
y
\end{pmatrix}
$$

Es decir, los multiplicadores de Lagrange son los autovalores $\lambda_1$ y $\lambda_2$ de la matriz $P^t\cdot P$, y los puntos $(x,y)$ que buscamos son los autovectores de norma 1 asociados a dichos autovalores. Además los valores máximos y mínimos de la función $f$ son:

$$
f(x,y)=\|P(x,y)\|^2 = \begin{pmatrix}
x\\
y
\end{pmatrix}^t \cdot P^t \cdot P \cdot \begin{pmatrix}
x\\
y
\end{pmatrix}= \begin{pmatrix}
x\\
y
\end{pmatrix}^t \cdot \lambda \begin{pmatrix}
x\\
y
\end{pmatrix}= \lambda \|(x,y)\|^2= \lambda
$$

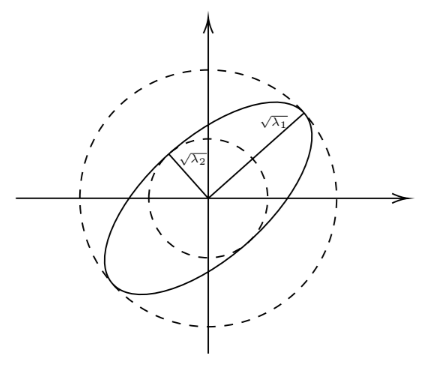
Obtenemos, como en la sección anterior, que la longitud de los semiejes son precisamente los valores singulares de la matriz $P$. Mientras que los ejes se encuentran en las rectas determinadas por la imagen por $P$ de los autovectores de $P^t\cdot P$.

Notemos que si $\sqrt{\lambda_1}$ es el valor singular mayor y $\sqrt{\lambda_2}$ es el menor, entonces:

$$
\sqrt{\lambda_1}=\sup \{\|P(x,y)\|: \|(x,y)\|=1\}
$$

$$
\sqrt{\lambda_2}=\inf \{\|P(x,y)\|: \|(x,y)\|=1\}
$$

cantidades conocidas en Ánalisis Funcional como la norma y la co-norma, respectivamente, de la aplicación lineal $P$. Es bien conocido que la norma anterior es realmente una norma en el espacio de las aplicaciones lineales, mientras que la co-norma no lo es. Desde el punto de vista geométrico, la circunferencia de centro el origen y de radio la norma de $P$ es la menor circunferencia que contiene a la elipse, mientras que la co-norma es el radio de la mayor circunferencia contenida en la elipse. La co-norma nos da idea de cómo de achatada es la elipse.

Notemos que si $P$ es una matriz singular, es decir no invertible, (y no nula) entonces la imagen por $P$ de todo $\mathbb R^2$ es una recta que pasa por el origen, por lo que la imagen de $S^1$ será un segmento centrado en el origen, es decir una elipse degenerada. En este caso, la co-norma de $P$ será $0$.

Grosso modo, podemos decir que cuanto más pequeña sea la co-norma de $P$ más cerca está esta matriz $P$ de ser singular, es decir, de que sus vectores columna sean linealmente dependientes.