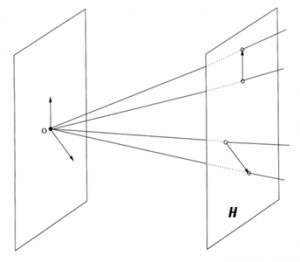
Los puntos del espacio proyectivo P de dimensión n son las rectas vectoriales del espacio vectorial V de dimensión n+1. Así, la recta proyectiva representa las direcciones del plano vectorial, y el plano proyectivo las direcciones del espacio vectorial. Si fijamos un hiperplano H de V que no pasa por el origen O, las rectas que pasan por O y no son paralelas a H se corresponden biyectivamente con los puntos de H. Las demás rectas, que pasan por O y son paralelas a H son los puntos de infinito de H. Se observa que los puntos de infinito constituyen a su vez un espacio proyectivo P’ de dimensión n-1. De este modo, P se descompone en el espacio afín H de dimensión n más el hiperplano de infinito P’.
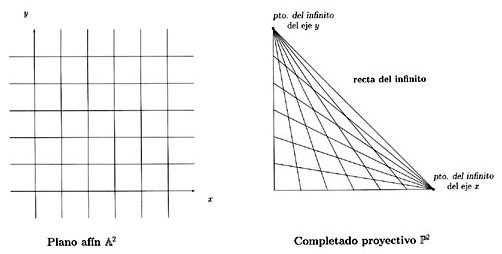
 Por ejemplo, la recta proyectiva es la recta afín más un punto de infinito, y el plano proyectivo es el plano afín más una recta (proyectiva) de puntos de infinito.
Por ejemplo, la recta proyectiva es la recta afín más un punto de infinito, y el plano proyectivo es el plano afín más una recta (proyectiva) de puntos de infinito.