En el contexto de sus investigaciones sobre Óptica, Johannes Kepler (1571-1630) introdujo en 1604 la noción de punto de infinito para dotar a la parábola de un segundo foco. Kepler estudia el comportamiento de una elipse tanto en el caso en el que los dos focos se junten dando lugar a una circunferencia, como en el caso en el que un foco quede fijo y el otro se aleje dando lugar a una parábola. ¿Dónde está entonces el segundo foco de la parábola? Kepler decía que en una parábola un foco estaba dentro y el otro a una distancia infinita del primero. No ocurre así en elipses ni hipérbolas, cuyos focos están a distancia finita.
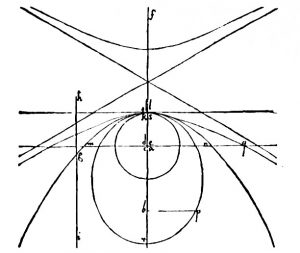
Sistema de cónicas de Kepler, 1604
Mientras que en la elipse y en la hipérbola los rayos de luz que parten de un foco se reflejan en rayos que pasan por el otro foco, en la parábola los rayos que parten del foco se reflejan en rayos paralelos al eje, y por tanto el foco segundo de la parábola está en ambas direcciones a lo largo del eje (tiene que estar en ambas para dar continuidad a las transformaciones de la elipse y la hipérbola en una parábola). Y ésta es justamente la idea de la noción moderna de los puntos de infinito.

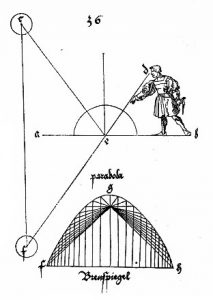
El estudio de Kepler sobre los focos de las secciones cónicas se enmarca en el problema de dar una teoría unificada para las investigaciones sobre reflexión y refracción de los rayos de luz en espejos cóncavos y convexos de tipo cónico. Euclides ya da razón de los llamados espejos ardientes, que eran espejos cóncavos tales que al concentrar los rayos de sol en el foco hacen que los objetos situados en éste entren en combustión. Kepler es muy conocido además por su demostración de que las órbitas de los planetas son elípticas.
Como anécdota se puede mencionar que el ocho tumbado que se utiliza para representar infinito se debe a John Wallis, matemático inglés del siglo XVII.






































