Como se sabe, dada una matriz \(A \in \mathbb M_{m\times n}\) de \(m\) filas y \(n\) columnas puede escribirse como

$$
A = USV^{T}
$$

donde \(U \in \mathbb M_{m}\) y \(V \in \mathbb M_{n}\) son matrices ortogonales (i.e. \(U^{T}U=I_m \), \(V^{T}V=I_n \)) y \(S \in \mathbb M_{m\times n}\) es una matriz diagonal. Una demostración sencilla de esto puede encontrarse en este artículo.

Si reescribimos la ecuación anterior como

$$
AV = US
$$

podemos interpretarla como que existe una base ortonormal de \(\mathbb R^n\) (las columnas de \(V\) ) que se transforma por \(A\) en una base ortogonal de \(\mathbb R^m\) (las columnas de \(U\), cada una de ellas multiplicada por el elemento correspondiente de la diagonal de \(S\) ).

De esta forma, la esfera unidad del primer espacio se convierte en un elipsoide en el segundo cuyos ejes son, precisamente, el citado sistema ortogonal en \(\mathbb R^m\).

Vamos a ver esto en el caso en que \(m,n=2\). Recordamos que, en el plano, las matrices ortogonales representan isometrías (una rotación alrededor del origen o una reflexión respecto a una recta que pasa por el origen).

---

Dada la matriz

$$ A = \begin{pmatrix}
1 & 1 \\
1 & -2
\end{pmatrix}
$$

su descomposición en valores singulares \( A = USV^{T}\) es

$$ U = \begin{pmatrix}
-0.2898 & 0.9571 \\
0.9571 & 0.2898
\end{pmatrix}
$$

$$ S = \begin{pmatrix}
2.3028 & 0 \\
0 & 1.3028
\end{pmatrix}
$$

$$ V = \begin{pmatrix}
0.2898 & 0.9571 \\
-0.9571 & 0.2898
\end{pmatrix}
$$

En la siguiente figura se muestra cómo varía la circunferencia unidad según se van multiplicando sus puntos por \( V^T\), \( S\) y \( U\). Los ejes que se dibujan son, respectivamente, las columnas de \( V\), sus transformados por \( V^T\) (es decir, la base canónica), la dilatación de esta como resultado de multiplicar por \( S\) y, finalmente, la rotación correspondiente a \( U\).

De esta forma, los ejes de la elipse en que se transforma la circunferencia unidad son los correspondientes a los vectores

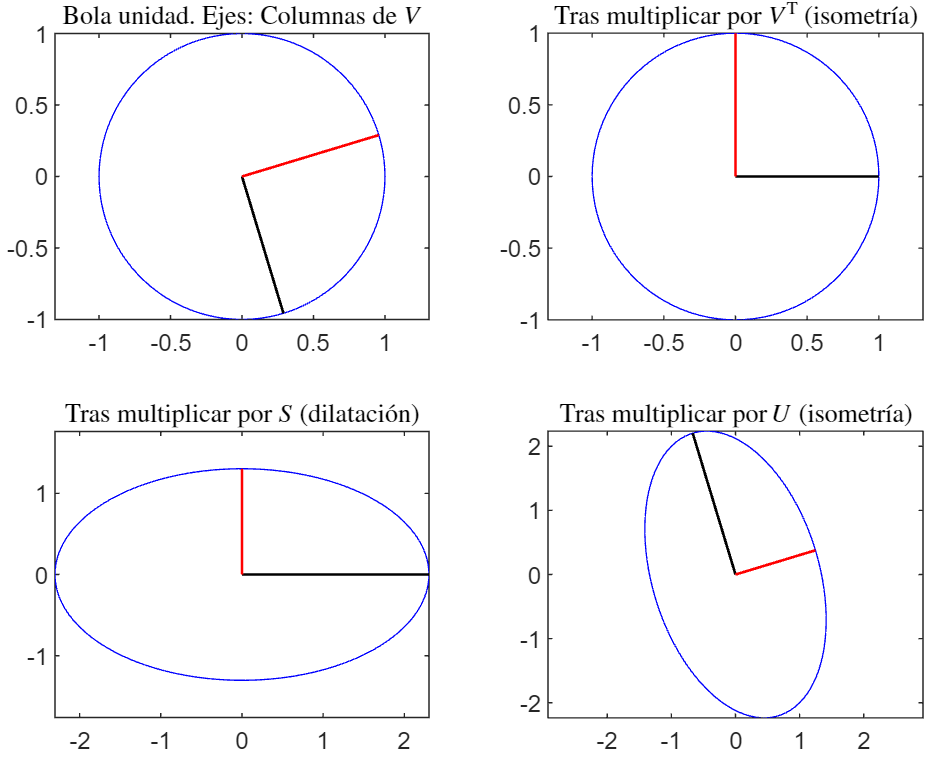
$$ E1 = \begin{pmatrix}
-0.6673 \\
2.2040
\end{pmatrix}
$$

de longitud \( 2.3028\) y

$$ E2 = \begin{pmatrix}
1.2469 \\
0.3775
\end{pmatrix}
$$

de longitud \( 1.3028\).

En este enlace puedes descargar el script Live Editor

---