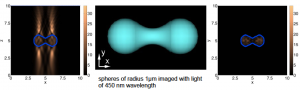
PDE constrained optimization methods in conjunction with topological sensitivity based techniques provide a powerful tool to reconstruct the geometry and properties of objects buried in a medium by scattering of electromagnetic, acoustic or thermal waves. The idea is to exploit the topological sensitivity of cost functionals defined in terms of the data measured at a set of receptors to produce first guesses of the objects. The procedure is robust to noise. When enough incident directions or frequencies are employed, a topological derivative based iteration may provide a reasonable description of the objects geometry. The method works with both harmonic or general time dependent incident radiations by either selecting different incident directions or recording information at different times. We have applied this strategy to acoustic sounding of bodies, electrical impedance tomography and photothermal imaging, combining it with optimization techniques to identify material parameters. We are able to generate good first approximations of the number, size and location of the scatterers, and improve the description of their shape and material parameters in a few steps. Making use of iteratively regularized Gauss-Newton techniques, we can invert holographic data in noninvasive light imaging of 3D biological samples. Resorting to Bayesian approaches, and either linearized posteriors about an optimal point or Markov Chain Monte Carlo sampling, we are able to quantify uncertainty in inversion processes (holography, elastography) for increasing noise magnitudes.
| Stability of object based full-waveform inversion schemes with respect to mesh choices, C. Abugattas, A. Carpio, E. Cebrián, G. Oleaga, submitted 2023 Object based Bayesian full-waveform inversion for shear elastography, A. Carpio, E. Cebrián, A. Gutiérrez, Inverse Problems 39, 075007, 2023 [pdf] [arxiv] Seeing the invisible: digital holography, A. Carpio, EMS Magazine 125, 4-12, 2022 [pdf] Pattern recognition in data as a diagnosis tool, A. Carpio, A. Simón, A. Torres, L.F. Villa, Journal of Mathematics in Industry 12, 3, 2022 [pdf][arxiv] Uncertainty quantification in covid-19 spread: lockdown effects, A. Carpio, E. Pierret, Results in Physics, 35, 105375, 2022 [pdf] [arxiv] Processing the 2D and 3D Fresnel experimental databases via topological derivative methods, A. Carpio, M. Pena, M.L. Rapún, Inverse Problems 37, 105012, 2021 [pdf] Multifrequency topological derivative approach to inverse scattering problems in attenuating media, A. Carpio, M.L. Rapún, Symmetry (Issue on Advanced Mathematical and Simulation Methods for Inverse Problems) 13, 1702, 2021 [pdf] Bayesian approach to inverse scattering with topological priors, A. Carpio, S. Iakunin, G. Stadler, Inverse Problems 36, 105001, 2020 [pdf] [arxiv] When topological derivatives met regularized Gauss-Newton iterations in holograhic 3D imaging, A. Carpio, T.G. Dimiduk, F. Le Louer, M.L. Rapun, Journal of Computational Physics 388, 224-251, 2019 [pdf][arxiv] Optimization methods for in-line holography, A. Carpio, T.G. Dimiduk, V. Selgas, P. Vidal, SIAM Journal on Imaging Sciences 11(2), 923-956, 2018 [pdf] [arxiv] Noninvasive imaging of three-dimensional micro and nanostructures by topological methods, A. Carpio, T.G. Dimiduk, M.L. Rapun, V. Selgas, SIAM Journal on Imaging Sciences 9(3), 1324-1354, 2016 [pdf] [arxiv] Measuring strain and rotation fields at the dislocation core in graphene, L.L. Bonilla, A. Carpio, C. Gong, J.H. Warner, Physical Review B 92(15), 155417, 2015 [pdf] [arxiv] Parameter identification in photothermal imaging, A. Carpio, M.L. Rapún, Journal of Mathematical Imaging and Vision 49 (2), 273-288, 2014 [pdf] [archivo] Hybrid topological derivative-gradient based methods for nondestructive testing, A. Carpio, M.L. Rapun, Abstract and Applied Analysis 816134, 2013 [pdf] Hybrid topological derivative and gradient-based methods for electrical impedance tomography, A. Carpio, M.L. Rapún, Inverse Problems 28(9), 095010, 2012 [pdf] [archivo] Determining planar multiple sound-soft obstacles from scattered acoustic fields, A. Carpio, B.T. Johansson, M.L. Rapún, Journal of Mathematical Imaging and Vision 36(2), 185-199, 2010 [pdf] [archivo] An iterative method for parameter identification and shape reconstruction, A. Carpio, M.L. Rapún, Inverse Problems in Science and Engineering 18(1), 35-50, 2010 [pdf] [archivo] Domain reconstruction using photothermal techniques, A. Carpio, M.L. Rapún, Journal of Computational Physics 227(17), 8083-8106, 2008 [pdf] [archivo] Solving inhomogeneous inverse problems by topological derivative methods, A. Carpio, M.L. Rapún, Inverse Problems, 24(4), 045014, 2008 [pdf] [archivo] Topological derivatives for shape reconstruction, A. Carpio, M.L. Rapún, Lecture Notes in Mathematics 1943, 85-133, 2008 [pdf] [archivo] |
