Por Manuel de León y Antonio Gómez Corral.- Esta entrada fue publicada en el blog Matemáticas y sus fronteras , el día 1 de junio de 2020.

Las técnicas matemáticas para evaluar la extensión y el impacto de una epidemia y ayudar a su control son muy variadas. Hemos comentado en este blog sobre modelos como el modelo SIR y sus variantes, o aquellos donde se usan cadenas de Markov. En ellos se mezclan herramientas determinísticas, construidas desde ecuaciones diferenciales, con estocásticas, basadas en la teoría de probabilidad y los procesos estocásticos. Pero existen otras técnicas matemáticas que demuestran ser muy útiles, son las series temporales.

 

Una serie temporal no es más que una colección de datos que tradicionalmente son recogidos en instantes de tiempo equidistantes (por ejemplo, los litros de lluvia recogidos cada día en un determinado lugar), aunque ésta sea sólo una de las diferentes situaciones con las que tratar en la práctica. Hay por lo tanto un aspecto clave y es precisamente la evolución de estos datos con el tiempo, no tratamos con sucesos aleatorios. Con una serie temporal se trata de analizar lo que ha ocurrido en el pasado, pero también poder predecir el futuro.

Los desarrollos teóricos del análisis de series temporales comenzaron con el estudio de los procesos estocásticos. La primera aplicación a datos puede atribuirse al trabajo de G. U Yule y J. Walker en las décadas de 1920 y1930. Es en esa época cuando se introduce la media móvil, de la que hablaremos a continuación, y posteriormente Herman Wold introduce su modelo ARMA (AutoRegressive Moving Average) para series estacionarias, aunque la explotación completa del modelo tuvo que esperar a los años 1970, cuando aparece un libro clásico en el tema, “Time Series Analysis”, escrito por G. E. P. Box y G. M. Jenkins.

Un aspecto clave en una serie temporal es conseguir los datos (y garantizar que estos sean fiables), organizarlos temporalmente de la manera adecuada, examinar las tendencias (crecimiento o decrecimiento) e identificar datos que parezcan discordantes. Otro aspecto importante es la existencia de estacionalidad en los datos, porque esa propiedad es una información relevante.

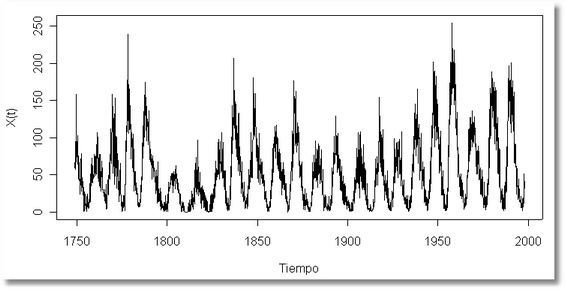
Esta imagen es una representación gráfica típica de una serie temporal, con los valores o datos en el eje de ordenadas y el tiempo en el eje de abscisas:

Esta otra se refiere a periodos plurianuales y podemos encontrarla actualizada en la web embalses.net.

Los datos se representan mediante una variable X, que depende del tiempo t, y se suele descomponer en tres contribuciones que se combinan y conducen, por ejemplo, a la relación

X_t = T_t + E_t + I_t,

donde la contribución T_t representa la tendencia, E_t es la parte estacional e I_t es la parte aleatoria. En concreto, E_t se denomina a veces señal, e I_t es el ruido. Esta descomposición está vinculada a un modelo aditivo. En general, tendríamos que referirnos a una función genérica de esas tres componentes, es decir,

X_t = f(T_t,E_t,I_t).

Por ejemplo, esa función podría ser el producto de las variables y tendríamos una serie multiplicativa

X_t = T_t · E_t · I_t .

En cualquier caso, lo que tratamos de conseguir al analizar una serie temporal es identificar si existen patrones de regularidad o no. Si no existieran, estaríamos ante un proceso aleatorio y no podríamos extraer mucha información.

Observar los datos para aprender sobre el modelo

A veces, la propia representación gráfica nos da mucha información y la visualización de los datos es un gran aliado a la hora de identificar el patrón de comportamiento. Pensemos, por ejemplo, en que representamos temperaturas mensuales en un proceso de cambio climático. Habrá fluctuaciones que mostrarán una tendencia creciente. Aunque esto es muy intuitivo, se pueden desarrollar métodos matemáticos que son bastante precisos a la hora de predecir temperaturas en instantes futuros.

Al representar los datos pretendemos, en un primer momento, descartar o no discontinuidades aparentes en la serie. En el caso de observar, por ejemplo, un cambio repentino de nivel de los datos puede ser aconsejable analizar la serie dividiéndola primero en segmentos homogéneos. Si hubiera observaciones extrañas, éstas deberían estudiarse cuidadosamente para verificar si hay alguna justificación para descartarlas; por ejemplo, si una observación ha sido grabada incorrectamente o responde efectivamente a las dinámicas de la serie temporal. La inspección del gráfico también debería sugerir la posibilidad de representar los datos como una realización del proceso (volvamos al ejemplo anterior con una descomposición lineal)

X_t = T_t + E_t + I_t,

donde el ruido aleatorio podría ser (débilmente) estacionario, en el sentido de que E[I_t] no depende de t y Cov(I_t, I_t+s) no depende de t, para cada s. Con esta propiedad se pretende que el valor promedio del ruido aleatorio registrado en un cierto instante no dependa del instante de observación y que el grado de correlación entre los ruidos observados en dos instantes de tiempo no dependa de esos instantes de tiempo, sino del tiempo transcurrido entre ellos. Cuando las fluctuaciones de la estacionalidad y el ruido aumentan con el nivel del proceso, es aconsejable realizar una transformación, por ejemplo, logarítmica de los datos para que los datos resultantes sean más compatibles con el modelo.

Supongamos que la relación X_t = T_t + E_t + I_t es el modelo apropiado, posiblemente después de una transformación preliminar de los datos. En tal caso, el objetivo sería estimar y extraer las componentes deterministas T_t y E_t, con la esperanza de que el residuo estocástico I_t sea una serie estacionaria en el tiempo. Entonces, podríamos usar la teoría de los procesos estacionarios para encontrar un modelo probabilístico satisfactorio para I_t, no sólo para estudiar sus propiedades, sino también para usarlo junto a T_t y E_t con el fin de predecir y simular X_t.

Otro enfoque, desarrollado ampliamente por G. E. P. Box y G. M. Jenkins (1976), consiste en aplicar operadores de diferenciación repetidamente a la serie X_t hasta que las observaciones diferenciadas se asemejen a la realización de alguna serie temporal estacionaria W_t. Entonces se usaría la teoría de los procesos estacionarios para el modelado, el análisis y la predicción de W_t y, por lo tanto, del proceso original.

Algunos elementos sencillos

La tendencia de una serie temporal puede estudiarse, a nivel preliminar, con lo que llamamos filtros o funciones que transforman la serie original en otra que nos da más información sobre la dada. Uno de esos filtros, probablemente el más simple, es la llamada media móvil. Por ejemplo, si damos tres valores consecutivos, X_t-1, X_t, X_t+1, la media móvil es

m(X_t) = (X_t-1 + X_t + X_t+1) / 3.

Pero ésta es solo una de las múltiples posibilidades. También podemos suavizar la serie tomando diferencias consecutivas, y esto lo podemos hacer recursivamente. Estos procesos de filtrado nos darán la información sobre la tendencia de la serie temporal.

El promedio móvil y el suavizado espectral son esencialmente métodos no paramétricos para la estimación de tendencias (o señales) y no para la construcción de modelos. La elección del filtro de suavizado requiere una buena dosis de juicio subjetivo y se recomienda que se pruebe una variedad de filtros para tener una buena idea de la tendencia subyacente. El suavizado exponencial, dado que se basa sólo en un promedio móvil de valores pasados, a menudo se usa para pronosticar, mientras que el valor suavizado en el momento actual es utilizado como el pronóstico del siguiente valor.

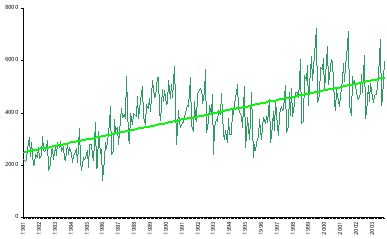
Otro método más expeditivo es determinar una recta (con generalidad, un polinomio) de regresión por el método de mínimos cuadrados, que nos daría una información gráfica como ésta:

Otra técnica de análisis en series temporales consiste en analizar sus cambios a lo largo del tiempo mediante las denominadas tasas de variación, que surgen de la comparación de los valores de la serie en dos periodos de tiempo distintos, por ejemplo,

∆X_t = X_t – X_t-1

y la tasa relativa

m_t = ∆X_t / X_t-1

que nos irá dando razón de su crecimiento o decrecimiento.

Para observar la estacionalidad, se puede emplear el coeficiente de autocorrelación, que no es más que el coeficiente de correlación de dos variables, pero ahora aplicado a los pares consecutivos de los valores de la serie

(X₁, X₂), (X₂, X₃), …, (X_t-1, X_t), (X_t, X_t+1), …

Esto nos da el coeficiente de correlación de orden 1; si tomamos pares separados por dos unidades, obtenemos el de orden 2 y, así sucesivamente, hasta que el número de datos lo permita.

Métodos de estudio

Por supuesto, estos elementos son sólo los más simples, como pretenden mostrar nuestros comentarios, de todos los usados en una amplia variedad de modelos de series temporales ARMA, ARIMA, SARIMA, modelos multivariantes y espacio-tiempo, entre otros, que podemos encontrar exhaustivamente estudiados en un buen número de monografías. Nosotros nos inclinamos por todo un clásico: el texto de J.P. Brockwell y R.A. Davis titulado “Introduction to Time Series and Forecasting”, publicado por Springer en sus sucesivas ediciones en los años 1996, 2002 y 2016.

En numerosas ocasiones, se pueden encontrar implementaciones en R de modelos de series temporales aplicadas a una variedad de ámbitos, como es el modelo SIR de epidemia. Bajo el término R (“The R Project for Statistical Computing”) se conoce un entorno de software libre para la computación estadística y gráfica, que compila y se ejecuta en una amplia variedad de plataformas UNIX, Windows y MacOS. La comunidad científica hace uso extensivo de este software y es común que los científicos pongan a disposición de sus colegas, de manera altruista, los códigos desarrollados en sus trabajos.

Son tantos los modelos de series temporales y tan variadas las técnicas de análisis que no podemos concluir esta entrada sin poner de manifiesto que la literatura sobre series temporales y su tratamiento analítico alude a una clasificación en:

• Métodos de dominio de frecuencia, donde se incluyen el análisis espectral y el análisis wavelet.
• Métodos de dominio de tiempo, que incluyen análisis de autocorrelación y correlación cruzada.

De manera paralela, la clasificación de las técnicas de análisis de series temporales conduce a:

• Los métodos paramétricos, donde se asume que el proceso estocástico estacionario subyacente tiene una determinada estructura que puede describirse utilizando un pequeño número de parámetros; por ejemplo, utilizando un modelo autorregresivo o de media móvil. Su objetivo entonces es estimar los parámetros del modelo que describe el proceso estocástico.
• Los métodos no-paramétricos, orientados a estimar explícitamente la covarianza o el espectro del proceso sin asumir que el proceso tiene una estructura particular.

Los métodos de análisis de series temporales también se pueden dividir en lineales y no lineales, como ya hemos comentado, y univariantes y multivariantes, en referencia a la dimensionalidad del proceso.

Métodos específicos versus métodos robustos

Habiendo nombrado el modelo SIR se nos viene a la cabeza el uso de las series temporales que nuestro colega Santiago García Cremades y el grupo de investigación de la Universidad Miguel Hernández, en Elche, están haciendo para predecir el número de fallecidos por SARS-CoV-2 en España. Ellos han constatado que los modelos SIR no sirven para describir las dinámicas de propagación de SARS-CoV-2 y no se debe a sus virtudes, que son muchas, sino a circunstancias ajenas al propio modelo, como son el confinamiento, las limitaciones de movilidad y, ante todo, la imprecisión de los datos diarios ofrecidos por las autoridades sanitarias.

Es muy oportuno el símil que, como buen divulgador, Santiago García Cremades hace para El Confidencial sobre el valor de las series temporales como un método de predicción robusto. En concreto, contrapone los modelos SIR con el análisis de la serie temporal comparando entre un microscopio y un telescopio, dos herramientas que permiten ver lo cercano (microscopio = modelos SIR) con un detalle específico y lo lejano (telescopio = series temporales) con un detalle más generalista.

Pero, vamos a lo importante: ¿qué se prefiere hoy frente a SARS-CoV-2, un método específico o un método robusto?

En las circunstancias actuales, un método robusto basado en series temporales y análisis multivariante tendrá mejores prestaciones que un método específico basado en los modelos SIR.

Los motivos son diversos, pero quizás no haya que escribir aquí muchos detalles matemáticos para que el lector de este blog lo comprenda. Brevemente, digamos que los modelos SIR se construyen sobre una colección de hipótesis que se mantienen invariables a lo largo del tiempo y que conducen a predicciones muy ajustadas, pero que se convierten en imprecisas cuando se modifican las hipótesis con el trascurso del tiempo. Para determinar las hipótesis o parámetros del modelo SIR es crucial disponer de un buen conocimiento de los episodios previos de la enfermedad – cosa que no ocurre con SARS-CoV-2 – y asegurar su validez en el tiempo. Por el contrario, las series temporales permiten “actualizar” las hipótesis a lo largo del tiempo con nuevos datos y, como consecuencia, aprender de la evolución de la pandemia con el paso del tiempo, sin necesidad (mejor dicho, con menor necesidad, si comparamos con los modelos SIR) de comprender los motivos que generan las fluctuaciones de los datos.