Sea \(\mathbb{R}^{m\times n}\) el conjunto de las matrices con \(m\) filas y \(n\) columnas.

Cuando trabajamos con observaciones, frecuentemente, nos encontramos con sistemas de ecuaciones lineales

$$
\mathbf{A}\mathbf{x}=\mathbf{y}
$$

con \(\mathbf{A}\in\mathbb{R}^{m\times n}\) y donde, por los errores de observación:

1. El número de observaciones \(m\) es mayor que el número de incógnitas \(n\).
2. El sistema de ecuaciones \(\mathbf{A}\mathbf{x}=\mathbf{y}\) es incompatible.
   [Sabemos que el sistema de ecuaciones \(\mathbf{A}\mathbf{x}=\mathbf{y}\) es incompatible \(\Leftrightarrow \mathbf{y} \not\in \text{Col}(\mathbf{A})\).]

Pero si los errores de observación son pequeños, el vector \(\mathbf{y}\) distará muy poco del espacio \(\text{Col}(\mathbf{A})\)
[ \(\text{Col}(\mathbf{A})\) es un subespacio de \(\mathbb{R}^{m}\)].
Esta proximidad sugiere que para estimar \(\mathbf{x}\) se reemplaza el vector \(\mathbf{y}\) por su proyección ortogonal sobre \(\text{Col}(\mathbf{A})\).

Llamamos \(\widehat{\mathbf{y}}\) a la proyección de \(\mathbf{y}\) sobre el espacio columna de \(\mathbf{A}\). Como \(\widehat{y}=\text{proy}_{\text{Col}(\mathbf{A})}(\mathbf{y}) \in \text{Col}(\mathbf{A})\) existirá un \(\widehat{\mathbf{x}}\) tal que \(\widehat{\mathbf{y}}=\mathbf{A}\widehat{\mathbf{x}}\), es decir: El sistema \(\widehat{\mathbf{y}}=\mathbf{A}\widehat{\mathbf{x}}\) es compatible.

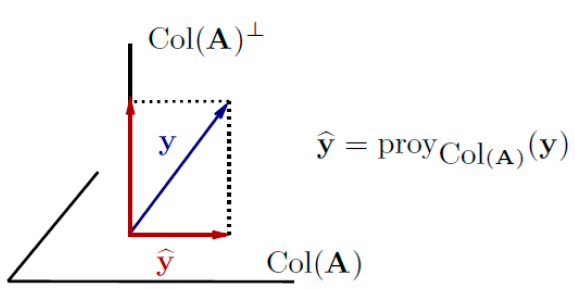
• Por el teorema de la mejor aproximación \(|\widehat{\mathbf{y}}-\mathbf{y}| \leq |\mathbf{w}-\mathbf{y}| \text{ } \forall \, \mathbf{w} \in \text{Col}(\mathbf{A})\),
• por tanto, las soluciones del sistema de ecuaciones \(\mathbf{A}\widehat{\mathbf{x}}=\widehat{\mathbf{y}}\) están caracterizadas por \(|\mathbf{A}\widehat{\mathbf{x}}-\mathbf{y}|^{2} \leq |\mathbf{A}\mathbf{x}-\mathbf{y}|^{2} \text{,} \quad \forall \, \mathbf{x} \in \mathbb{R}^{n}.\)
• Si denotamos\(\mathbf{r}(\mathbf{x}) = \mathbf{A}\mathbf{x}-\mathbf{y} = \begin{pmatrix} r_{1}(\mathbf{x}) \\ \vdots \\ r_{m}(\mathbf{x})\end{pmatrix}\)teniendo en cuenta que$$
  |\mathbf{A}\mathbf{x}-\mathbf{y}|^{2}=\begin{pmatrix}r_{1}(\mathbf{x}) & \ldots & r_{m}(\mathbf{x})\end{pmatrix}\begin{pmatrix}r_{1}(\mathbf{x}) \\ \vdots \\ r_{m}(\mathbf{x})\end{pmatrix}=\sum_{i=1}^{m}r_{i}(\mathbf{x})^{2}
  $$la desigualdad anterior se reescribe como:$$
  \sum_{i=1}^{m}r_{i}(\widehat{\mathbf{x}})^{2} \leq \sum_{i=1}^{m}r_{i}(\mathbf{x})^{2}
  $$

  ---

  Por tanto, las soluciones del sistema \(\mathbf{A}\widehat{\mathbf{x}}=\widehat{\mathbf{y}}\) tienen la propiedad de ser los puntos \(\widehat{\mathbf{x}} \in \mathbb{R}^{n}\) donde la suma de los cuadrados de las componentes del vector \(\mathbf{A}\mathbf{x}-\mathbf{y}\) alcanza su mínimo.

  ---

  En términos generales, resolver un problema en el sentido mínimos cuadrados es sustituir un problema en el que hay que resolver un sistema de ecuaciones que no tiene solución por el problema de minimizar una suma de cuadrados.

Sean \(\mathbf{A}\in \mathbb{R}^{m\times n}\) e \(\mathbf{y}\in \mathbb{R}^{m}\). Un vector \(\widehat{\mathbf{x}}\in \mathbb{R}^{n}\) es una solución mínimos cuadrados del sistema de ecuaciones lineales \(\mathbf{A}\mathbf{x}=\mathbf{y}\) si

$$
\mathbf{f}(\widehat{\mathbf{x}})\leq \mathbf{f}(\mathbf{x})
$$

para todo \(\mathbf{x}\in \mathbb{R}^{n}\), donde \(\mathbf{f}(\mathbf{x})=| \mathbf{A}\mathbf{x}-\mathbf{y}|^{2}\).

Dado un sistema de ecuaciones \(\mathbf{A}\mathbf{x}=\mathbf{y}\), con \(\mathbf{A}\in \mathbb{R}^{m\times n}\) e \(\mathbf{y}\in \mathbb{R}^{m}\).
Sea \(\widehat{\mathbf{x}}\in \mathbb{R}^{n}\).

\(\widehat{\mathbf{x}}\) es solución mínimos cuadrados de \(\mathbf{A}\mathbf{x}=\mathbf{y} \Leftrightarrow \widehat{\mathbf{x}}\) es solución del sistema de ecuaciones (compatible)

$$
\mathbf{A}^{T}\mathbf{A}\,\widehat{\mathbf{x}}=\mathbf{A}^{T}\mathbf{y}
$$

Este sistema se denomina sistema de ecuaciones normales asociado al sistema de ecuaciones \(\mathbf{A}\mathbf{x}=\mathbf{y}\).

---

1. Si \(\text{rango}(\mathbf{A})=n\), el sistema de ecuaciones normales es compatible determinado y, por tanto, el sistema \(\mathbf{A}\mathbf{x}=\mathbf{y}\) tiene una única solución mínimos cuadrados:$$
   \widehat{\mathbf{x}}=\mathbf{A}^{+}\mathbf{y} \qquad \text{con } \mathbf{A}^{+}=(\mathbf{A}^{T}\mathbf{A})^{-1}\mathbf{A}^{T}
   $$
2. Si \(\text{rango}(\mathbf{A})<n\), el sistema de ecuaciones normales es compatible indeterminado y, por tanto, \(\mathbf{A}\mathbf{x}=\mathbf{y}\) tiene infinitas soluciones mínimos cuadrados (coinciden con las soluciones del sistema de ecuaciones normales).</p

El vector \(\widehat{\mathbf{y}} \doteq \text{Proy}_{\text{Col}(\mathbf{A})}(\mathbf{y})=\mathbf{A}\widehat{\mathbf{x}}\) se denomina vector de observaciones ajustadas.

---

Observar que las siguientes afirmaciones son equivalentes:

• El sistema \(\mathbf{A}\mathbf{x}=\mathbf{y}\) tiene una única solución mínimos cuadrados.
• La matriz \(\mathbf{A}^{T}\mathbf{A} \in \mathbb{R}^{n \times n}\) es definida positiva.
• El único elemento del espacio nulo es el vector cero (\(\text{dim}(\text{Nul}(\mathbf{A}))={0}\)).
• Los vectores columnas de \(\mathbf{A}\) son linealmente independientes.
• \(\text{rango}(\mathbf{A})=n\).

Consideramos el sistema \(\mathbf{A}\mathbf{x}=\mathbf{y}\), con \(\mathbf{A} \in \mathbb{R}^{m \times n}\) tal que \(\text{rango}(\mathbf{A})=m<n\).
En esta situación:

• El sistema \(\mathbf{A}\mathbf{x}=\mathbf{y}\) es compatible y tiene infinitas soluciones:
• \(\mathbf{A}\mathbf{A}^{T}\) es definida positiva.

Buscamos, entre las infinitas soluciones del sistema compatible indeterminado \(\mathbf{A}\mathbf{x}=\mathbf{y}\) la solución de norma más pequeña.

---

La solución norma mínima del sistema compatible indeterminado \(\mathbf{A}\mathbf{x}=\mathbf{y}\) es:

$$
\widehat{\mathbf{x}}=\mathbf{A}^{+}\mathbf{y}
$$

con \(\mathbf{A}^{+}=\mathbf{A}^{T}(\mathbf{A}\mathbf{A}^{T})^{-1}\). Esta solución es única.

El concepto de pseudoinversa de una matriz es una generalización del concepto usual de inversa para matrices cuadradas.

Sea \(\mathbf{A}\in\mathbb{R}^{m\times n}\). Si \(\mathbf{A}^{+}\in\mathbb{R}^{n\times m}\) es una matriz tal que:

1. \(\mathbf{A}\mathbf{A}^{+}\mathbf{A}=\mathbf{A}\)
2. \(\mathbf{A}^{+}\mathbf{A}\mathbf{A}^{+}=\mathbf{A}^{+}\)
3. \(\mathbf{A}\mathbf{A}^{+}\) es simétrica
4. \(\mathbf{A}^{+}\mathbf{A}\) es simétrica

se dice que \(\mathbf{A}^{+}\) es la matriz pseudoinversa de \(\mathbf{A}\) (o inversa de Moore-Penrose).

---

Toda matriz \(\mathbf{A}\in\mathbb{R}^{m\times n}\) tiene pseudoinversa y, además, ésta es única.

---

La pseudoinversa se puede calcular a partir de la Descomposción en Valores Singulares. Si

$$
\mathbf{A} = \mathbf{U}\mathbf{S}\mathbf{V}^T
$$

entonces

$$
\mathbf{A}^{+} = \mathbf{V}\mathbf{S}^{*}\mathbf{U}^T
$$

donde \(\mathbf{S}^{*}\) se forma a partir de \(S\) tomando el recíproco de todos los elementos distintos de cero, dejando todos los ceros solos y haciendo que la matriz tenga la forma correcta:
Si \(S\) es una matriz de \(m \times n\), entonces \(\mathbf{S}^{*}\) debe ser una matriz de \(n \times m\).

Todo sistema de ecuaciones lineales \(\mathbf{A}\mathbf{x}=\mathbf{y}\) tiene:

• una única solución mínimos cuadrados-norma mínima, \(\mathbf{x}_{0}=\mathbf{A}^{+}\mathbf{y}\).
• al menos una solución mínimos cuadrados.