Research

Mathematical discussions during lunch in early 2020 at the Campus of the University of California San Diego, where I spent six wonderful years, first as a Tenured Associate Professor (2014-2018) and then as Full Professor (2018-2020).

Below I give a brief summary of my research according to topics. Along the way I refer to some of my papers, all of which can be found in the Publications section of the website. My research has been mainly supported by the National Science Foundation of USA in the period 2007-2020 and since 2022 by the BBVA Foundation in Spain.

SYMPLECTIC GEOMETRY OF CLASSICAL INTEGRABLE SYSTEMS

The unifying theme of this area is the use of analytic, geometric, or dynamical techniques to construct symplectic invariants of finite dimensional integrable Hamiltonian systems, and then use these invariants to better understand the system at all levels: classical, quantum, in applications to mechanics, robotics, quantum chemistry, engineering, etc. I recommend my paper with Vu Ngoc in Bulletin of the American Mathematical Society 2011 for a more in depth discussion along these lines and my BBVA Foundation paper 2024 for a general audience introduction (in Spanish) to symplectic geometry.

Since 2006 I have been mostly working on different aspects of finite dimensional dimensional integrable systems, and particularly interested in using symplectic methods to construct invariants of finite-dimensional integrable systems of so called semitoric type: these are systems with 2 degrees of freedom on 4-dimensional manifolds and for which one of the Hamiltonians generates a periodic motion. In collaboration with Vu Ngoc I proved, in Inventiones Mathematicae 2009 and Acta Mathematicae 2011, that semitoric systems are classified in terms of five invariants.

Semitoric systems retain some of the rigidity of toric systems but may have in addition nodal singularities (corresponding to singular fibers which are multipinched tori). Semitoric systems model some simple physical systems such as the spherical pendulum or the coupled spin-oscillator (known as Jaynes-Cummings model in quantum optics). I have worked extensively on semitoric systems since 2006, in collaboration with Vu Ngoc, with my former doctoral students Palmer and Tang, and also with Figalli and Ratiu. The results of these works have appeared, among others, in journals such as  Journal of Symplectic Geometry 2015, Journal of Nonlinear Science 2016, Nonlinearity 2017, Annali della Scuola Normale Superiore di Pisa 2018.

Recently, in a paper with Tang, published in the Journal of Fixed Point Theory and Applications in 2024, we classified the singular fibers of integrable systems which are tori with multiple pinched points, and then with Palmer and Tang we used this result to give a classification of non-simple semitoric systems in arXiv:1909.03501v2 (essentially these are semitoric systems without the restriction on having only one pinched point per focus-focus fiber).

An important related problem is to understand the structure of the moduli spaces that integrable systems form. In this direction I have been interested in endowing these “sets” with topological, symplectic or metric structures. With the aid of these structures, one can raise new questions about them, for which regularity questions may now be posed. In some cases these structures lead us to constructing new invariants. With several collaborators I have published papers in this direction, see Geometriae Dedicata 2014, Journal of Geometry and Physics 2018, and the 2023 preprint arxiv:2303.02369. This preprint shows that, in contrast with the work of Oda in dimension 4, one cannot expect a classification of minimal models of toric integrable systems in higher dimensions, and gives a proof of the connectivity of their moduli space in arbitrary dimension.

SPECTRAL GEOMETRY AND SEMICLASSICAL ANALYSIS OF QUANTUM INTEGRABLE SYSTEMS

This topic is connected at a very deep level with the previous one, so the separation is a little artificial (nonetheless the techniques can be very different) see Tao‘s answer to Why is symplectic geometry so important in modern PDE? The following is extracted from Tao‘s response:

“One of the great insights of quantum mechanics (or, on the mathematical side, semi-classical analysis) is the correspondence principle that asserts, roughly speaking, that the behaviour of quantum observables converges in the high-frequency limit (or, after rescaling, the semi-classical limit) to the analogous behaviour of classical observables. The correspondence is easier to see on the observable side than on the physical space side, for instance by connecting the von Neumann algebra of bounded quantum observables with smooth symbol with the Poisson algebra of smooth classical observables. The former is connected to linear PDE and the latter to symplectic (or Hamiltonian) geometry.”


In the 1970s and 1980s Colin de Verdière, Duistermaat, Guillemin, and Sjostrand, proved a series of major results in spectral theory of (differential, pseudodifferential) operators. Among the most striking ones are Colin de Verdiere‘s inverse results for collections of commuting pseudodifferential operators on cotangent bundles. The problems in this area belong to the realm of classical questions in inverse spectral theory going back to these pioneer works.

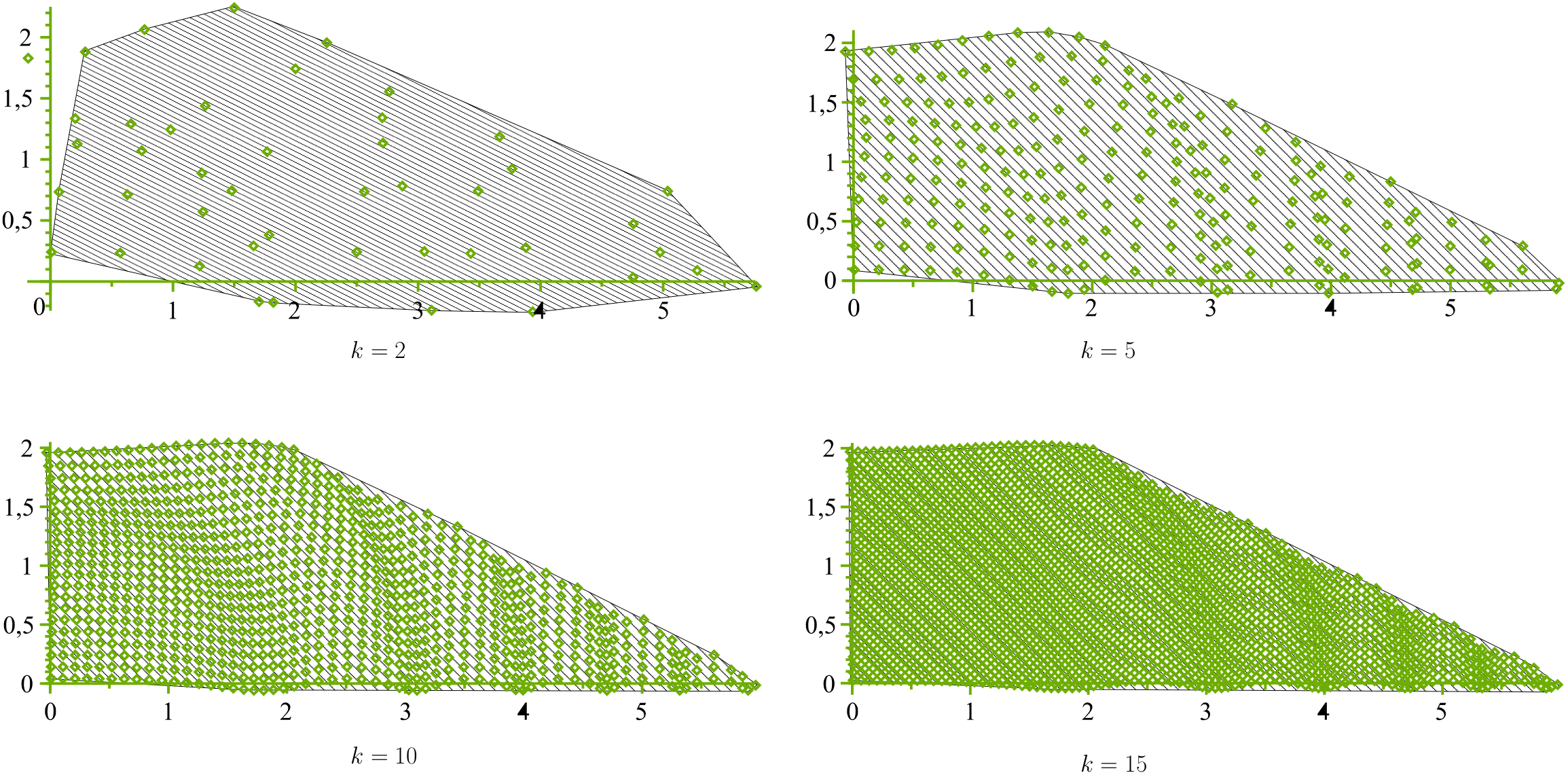
Semiclassical spectrum.

The figure shows the semiclassical spectrum of a quantum integrable system of toric type, for some values of the spectral parameter. In the semiclassical (high frequency) limit, this semiclassical spectrum converges to the classical spectrum, which in this case is a Hirzebruch trapezoid. By Delzant’s theorem, this trapezoid determines the symplectic geometry of the associated classical toric system.

In recent years a main focus of my research has been concerned with studying semiclassical spectral theory of quantum integrable systems using microlocal analysis for pseudodifferential operators and Berezin-Toeplitz operators. Microlocal analysis is a branch of analysis which establishes a deep connection between symplectic geometry and partial differential equations (it is connected at its core with harmonic analysis and representation theory). Even though quantum integrable systems date back to the early days of quantum mechanics, such as the work of Bohr, Sommerfeld and Einstein, the theory did not blossom at the time. The development of semiclassical analysis with microlocal techniques in the last forty years now permits a constant interplay between spectral theory and symplectic geometry. The goal of my research in this area has been to use this interplay between symplectic geometry and partial differential equations to prove inverse results about quantum systems.

I have been working on inverse spectral problems for quantum integrable systems, that is, studying when the semiclassical joint spectrum of the system, given by a sequence of commuting Berezin-Toeplitz or pseudodifferential operators on a sequence of Hilbert spaces, determines the classical integrable system given by the symplectic manifold and commuting Hamiltonians. My work at the intersection of symplectic and spectral geometry suggests that symplectic invariants are better encoded in spectral information than Riemannian invariants (Charles, myself, and Vu Ngoc have proved this for quantum toric systems in Annales Scientifiques de l’ Ecole Normale Superieure 2013).

The question of isospectrality in Riemannian geometry may be traced back to Weyl (1910) and is most well known thanks to an article by Kac (1966), who himself attributes the question to Bochner. Kac popularized the sentence: “can one hear the shape of a drum?”, to refer to this type of isospectral problem. Bochner and Kac‘s question has a negative answer in this case, even for planar domains with Dirichlet boundary conditions; major results in this direction were proven Osgood-Phillips-Sarnak, and Zelditch, among others. An important observation of Sarnak is that in this context a much better question to ask is whether the set of isospectral domains is finite or compact.

The following are specific topics I have worked on:

  • Spectral theory for singularities: studying the semiclassical spectral theory of singularities of quantum integrable systems, combining analytic methods developed in the past fifteen years in semiclassical analysis with results from symplectic geometry going back to the foundational works of Weinstein in the 1970s. I wrote two papers in this direction, with Vu Ngoc, for the case of focus-focus singularities, published in Communications in Mathematical Physics 2012 and Communications in Mathematical Physics 2014.
  • Global spectral theory for quantum integrable systems: studying direct and inverse spectral theory for quantum integrable systems. In some cases one can prove that the semiclassical spectrum of a quantum integrable system determines the classical system given by the principal symbols, or in other words, that one can hear integrable systems.  My main results, which are inspired by Colin de Verdière‘s inverse spectral results on pseudodifferential operators, are the following.
    • Inverse spectral theory for quantum toric systems: a proof that one can hear the only invariant, the Delzant polytope, of toric systems on compact manifolds. Hence by a classification due to Delzant (1988) of compact toric systems in terms of these Delzant polytopes, one can hear compact toric systems. I published this result with Charles and Vu Ngoc in Annales Scientifiques de l’ Ecole Normale Superieure 2013 and with Polterovich and Vu Ngoc in Proceedings of the London Mathematical Society 2014.
    • Inverse spectral theory for quantum semitoric systems: a proof that one can hear the first four invariants of semitoric systems, started in joint work with Vu Ngoc in Comunications in Mathematical Physics 2014, and completed in joint work with Le Floch and Vu Ngoc in Mathematische Annalen 2016. Hence, by the classification of semitoric systems, one can hear semitoric systems within the class of systems with the same fifth invariant. These contributions and related problems are discussed in my paper in Topology and Its Applications 2023.
  • Quantization of integrable systems: studying the existence of different types of quantizations and for different types of classical systems (Annales Scientifiques de l’ Ecole Normale Superieure 2013). I have also been interested in the connections to important works on the more algebraic side by Reshetikhin, Yakimov, and others.
  • Quantum integrable systems from physics: I have worked on understanding quantum versions of physical systems typical in mechanics (see Marsden and Ratiu book for several examples). This includes the Jaynes-Cummings model from quantum optics. For works in this direction see my paper with Vu Ngoc in Communications in Mathematical Physics 2012 and my paper with Le Floch in Journal of Nonlinear Science 2019.

APPLICATONS OF SYMPLECTIC TECHNIQUES TO TOPOLOGY AND DYNAMICAL SYSTEMS

In 1985 Gromov revolutionatized symplectic geometry by introducing pseudoholomorphic curves and using them to prove the celebrated Symplectic Nonsqueezing theorem: you cannot squeeze a big ball into an infinite thin cylinder by means of a symplectic map, or a Hamiltonian flow (even though the cylinder has infinite volume). Gromov proved this result by studying properties of moduli spaces of pseudoholomorphic curves. Gromov‘s Nonsqueezing result may also be interpreted as a strong instability result for Hamiltonian differential equations. Coming from the variational theory of Hamiltonian dynamics, Ekeland and Hofer gave a proof of Gromov‘s Nonsqueezing Theorem by studying periodic solutions of Hamiltonian systems. Hofer and Ekeland-Hofer introduced new invariants of symplectic manifolds, the so called symplectic capacities.

The specific topics I have worked on are:

  • Symplectic fixed points in the random setting: the interaction between random and deterministic ideas in dynamics is a highly active topic of research, see for instance the recent work of Bourgain–Sarnak–Ziegler (2013), and Sarnak‘s Lectures (2011) on “Mobius function Randomness and Dynamics”. I have studied the generalization of the Poincare–Birkhoff Fixed Point Theorem to area-preserving twist maps that are random with respect to a given probability measure. While random dynamics has been explored quite throughly, eg. Brownian motions, the implications of the area-preservation assumption remain relatively unknown. I have explored random versions of theorems in symplectic geometry using a theory of random generating functions introduced jointly with Rezakhanlou, following Chaperon and Viterbo. Our paper appeared in Transactions of the Mathematical Society in 2018. Most recently, in our 2023 preprint arXiv:2306.15586,  Rezakhanlou and I have taken the first steps to develop Conley-Zehnder Theory, as conjectured by Arnold, in the world of probability. This work provides, as far as we know, the first probabilistic theorems about the density of fixed points of symplectic twist maps in dimensions greater than two.
  • Symplectic stability of paths: studying stability problems for families of symplectic forms in the noncompact case, as analogs of Moser’s symplectic stability. I worked with Curry and Tang on proving that symplectic stability holds under natural growth conditions on the path of symplectic forms, some of our results in this direction may be found in Journal of Symplectic Geometry 2019 and Journal of Geometric Analysis 2019.
  • Existence or inexistence of symplectic embeddings: studying the existence or inexistence of symplectic embeddings of balls and cylinders into balls and cylinders, following Gromov, Polterovich, Guth, Hind-Kerman. These results have consequences in terms of symplectic capacities. They may also be interpreted in terms of stability (or instability) of Hamiltonian differential equations, following the works of Kuksin and Bourgain in the 1990s. At the invitation of Luis Caffarelli and Alessio Figalli I gave talks on this viewpoint which is perhaps less known in geometry at the PDE Seminar at the University of Texas in Austin, and at the conference honoring Alan Weinstein in July 2013. With Vu Ngoc I wrote two papers in this direction, published in Proceedings of the London Mathematical Society in 2015 and Indagationes Mathematicae in 2016. Similar questions may be considered in an equivariant setting, for example my paper in Proceedings of the American Mathematical Society 2007 studies the topology of moduli spaces of equivariant symplectic ball embeddings.  Recent progress in this direction appears in my paper with Figalli and Palmer in Annali della Scuola Normale Superiore di Pisa 2018.
  • Immersed symplectic surfaces: I used pseudoholomorphic curves in my paper with Coffey and Kessler in Annals of Global Analysis and Geometry 2012 in which we define a closed and non-degenerate 2-form on the space of immersed symplectic surfaces and give applications.

SYMPLECTIC AND HAMILTONIAN GROUP ACTIONS

In 1982 Atiyah and independently Guillemin & Sternberg proved one of the most influential results in the equivariant symplectic theory of group actions: the momentum map (introduced by Lie, Kostant, and Souriau) image of the action of a compact connected abelian Lie group (i.e. a torus) equals the convex hull of the images of the action fixed points, in particular it is convex. A school was created around this topic which flourished, and the area of Hamiltonian group actions is now a mainstream topic in equivariant symplectic geometry. I recommend my paper in Bulletin American Mathematical Society 2017 for an introduction to this area.

Several classification results have been achieved since, which involve some form of the momentum map image as an invariant. If one drops the condition on the action to be Hamiltonian (that is we no longer have a momentum map) the convexity result does not hold. However, it is still possibly to classify such actions in some cases which are of interest both in complex algebraic geometry (for instance the Kodaira variety falls into this class), and in symplectic topology. I worked on several of these cases.

Shortly after the work of Atiyah and Guillemin & Sternberg, Duistermaat and Heckman (1982) proved the DH Theorem which has extensive applications in geometry and analysis. This influential result expresses the Fourier transform of the push-forward of the Liouville measure by the momentum map (DH measure) of a Hamiltonian torus action in terms of the behavior around the fixed points (assumed isolated).

Hans Duistermaat, one of the foremost Dutch mathematicians of the twentieth century, and myself, at the Duistermaat’s residence in The Netherlands, in 2006. We wrote four joint papers. For more on Duistermaat’s contributions see “Remembering Johannes J. Duistermaat (1942-2010)” edited by V. Guillemin, myself, S. Vu Ngoc, and A. Weinstein, which is available in the Publications section. I consider Duistermaat to be the main influence on my mathematical career.

In 1984 Atiyah and Bott generalized the DH Theorem (to include non isolated points) and presented it using the far reaching setting of equivariant cohomology. Several of the problems I have worked on in this area concern the so called logarithmic concavity conjecture, which asks when the logarithm of the DH measure is a concave function. Although this is not in general true (proved by Karshon), it holds in important cases.

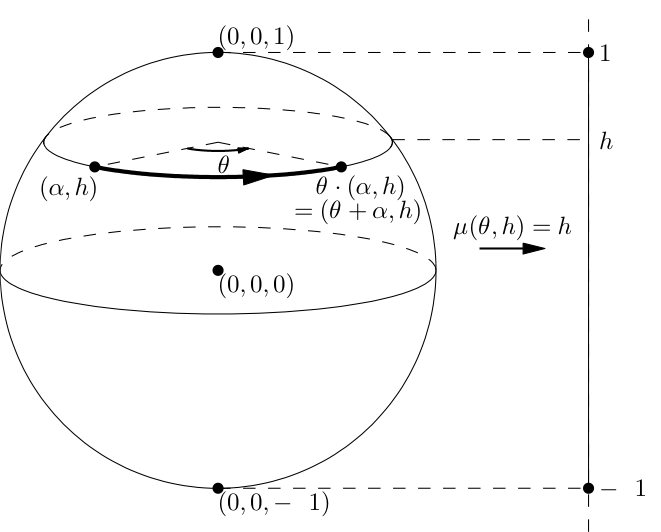
The figure shows the momentum map of the Hamiltonian action of the circle, by rotations about the vertical axis, on the standard 2-sphere. The momentum map is the height function on the sphere and the image of the momentum map is a compact interval. This interval is equal to the convex hull of the images under the momentum map of the fixed points of the action (the South and North poles of the sphere), as the convexity theorem of Atiyah and Guillemin-Sternberg states.

I have worked on the following specific topics:

  • Mononote toric geometry: monotone polytopes are associated to monotone toric manifolds and Gorenstein Fano toric varieties. In the 2023 preprint arxiv:2310.10366 with Crespo and Santos we prove a broad case of Ewald‘s Conjecture (1988) concerning lattice monotone polytopes as well as  the two-dimensional case of the closely related Nill’s Conjecture (2009). In a 2023 preprint in collaboration with Santos, arXiv:2308.03085, we answer a question of McDuff (2011) in this area.
  • Poisson toric geometry: going back to the pioneer work of Weinstein in Poisson geometry, I worked with Gualtieri, Li, and Ratiu on extending to the Poisson setting the classical theory of symplectic toric manifolds; our results appeared in a paper in Mathematische Annalen 2017.
  • Logarithmic Concavity Conjecture: studying in which settings the logarithmic concavity conjecture holds; the main tool is Hodge theory, see my paper with Lin in Mathematical Research Letters 2015.
  • Kosniowski Conjecture: this conjecture (1979) relates the existence of fixed points to the Hamiltonian character of a circle action on a compact manifold, when the fixed points are isolated. Full solutions are due to Frankel for compact Kahler manifolds and to McDuff for compact symplectic 4-manifolds. I have worked on the remaining cases of this conjecture with Godinho and Sabatini using Atiyah-Bott localization in equivariant cohomology and equivariant K-theory, in our paper in Communications in Number Theory and Physics 2015.
  • Symplectic fiber bundles: proving that symplectic non- Hamiltonian actions whose orbits are symplectic can be viewed as symplectic orbifold bundles over an orbifold. The base of the orbifold and the monodromy of the flat connection over it (given by the symplectic orthogonal complements to the tangent spaces to the orbits), essentially classify them. These results appeared in my paper in Memoirs of the American Mathematical Society 2010.
  • Existence of invariant Kahler and complex structures: Delzant classified in 1988 Hamiltonian actions of n-tori on compact 2n-dimensional manifolds (for any natural number n); I extended this result to symplectic, non-necessarily Hamiltonian actions of tori when 2n=4. As a consequence, one can determine which compact symplectic 4-manifolds endowed with torus actions admit complex and/or Kahler structures which are also invariant under the action; this is done by using a dictionary between the symplectic and complex analytic theory, using Kodaira‘s classification of complex analytic surfaces. These results, in collaboration with Duistermaat, appeared in our paper in the International Journal of Mathematics 2011.
  • Lagrangian and symplectic actions: studying symplectic non-necessarily Hamiltonian actions with Lagrangian orbits (which includes all Hamiltonian torus actions with maximal dimensional orbits); more generally study (and classify) symplectic actions whose orbits are coisotropic manifolds. Such manifolds include the Kodaira variety (also known as Kodaira-Thurston manifold). The study of such actions involves classical geometry going back to the foundational results of Cartan, Haefliger, Koszul, and Weinstein as well as more recent work of Benoist and others. In collaboration with Duistermaat I gave a symplectic classification of compact manifolds endowed with symplectic actions with coisotropic (or Lagrangian) principal orbits in our paper published in the Annales de l’Institut Fourier 2007. In my paper in Memoirs of the American Mathematical Society 2010 I built on this paper to give a symplectic classification of all symplectic actions of 2-dimensional tori on compact 4-dimensional manifolds.

HOMOTOPY TYPE THEORY

Homotopy type theory is a recently created field of mathematics which interprets type theory from a homotopical perspective. An introduction to this area may be found in my paper with Michael Warren published in the Bulletin of the American Mathematical Society 2014. Voevodsky‘s univalent foundations program is a research theme based on homotopy type theoretic ideas, and which can be carried out in a computer proof assistant. Sadly Voevodsky passed away in 2017 and I am myself no longer as active on this topic of research as I once was, although I still have a strong interest in seeing the theory of p-adic integrable systems implemented in this setting, as Voevodsky, Warren, and myself initiated in our paper published by Mathematical Structures in Computer Science 2015. I hope to return to this in the not too distant future.

The goal of Voevodsky‘s program is developing mathematics in the setting of type theory with an additional axiom which he introduced, the Univalence Axiom. Homotopy type theory is connected to several topics of interest in modern algebraic topology, such as infinity-groupoids and Quillen model structures. Awodey, myself, and Warren worked on explaining in non-specialized, non-technical, terms some of the basic literature on homotopy type theory and Voevodsky‘s univalent foundations program (which requires knowledge of homotopy theory and mathematical logic) making en emphasis on the connections to other branches of mathematics and theoretical computer science, see our paper published in Notices of the American Mathematical Society 2013.

Type theory was invented by Russell (1908), but it was first developed as a rigorous formal system by Church (1930s, 1940s). It now has numerous applications in computer science, especially in the theory of programming languages. In type theory objects are classified using a primitive notion of “type”, similar to the data-types used in programming languages. And as in programming languages, these elaborately structured types can be used to express detailed specifications of the objects classified, giving rise to principles of reasoning about them.

In homotopy type theory, one regards the types as spaces, or homotopy types, and the logical constructions as homotopy-invariant constructions on spaces. In this way, one is able to manipulate spaces directly, without first having to develop point-set topology or even define the real numbers. I hope that in the future, because this development of mathematics can be carried out in a proof assistant such as Coq so that the proofs carry some algorithmic content, it will be possible to extract good algorithms from the proofs. One of my motivations for the construction of the aforementioned algorithms is to help solve some problems concerning operator theory and integrable systems which are of particular interest in applications. For instance, one outstanding problem is: given numerical spectral data about a p-adic quantum system (coming from an experiment), extract an algorithm to reconstruct the classical integrable system. Voevodsky, myself, and Warren took the first steps in this direction by giving a homotopy type theoretic construction of the p-adic numbers in the setting of Voevodsky‘s univalent foundations (we also implemented the construction in the Coq proof assistant). The construction involves a univalent description of basic results in number theory and group theory.

From a symplectic geometry perspective, that is, without regard to homotopy type theory, a p-adic symplectic form may be defined as in the real case. The closedness condition makes sense in the p-adic setting, and so does the non-degeneracy condition (in fact, over any field). In the real setting, a theorem of Darboux says that all symplectic forms are locally equivalent, so real symplectic manifolds have no local invariants. It is natural to wonder whether this result holds in the p-adic setting “as is”. One should restrict to the analytic setting since the closedness condition is a system of differential equations. My initial motivation to work on the symplectic p-adic setting was with an eye on the future development and univalent implementation of a theory of p-adic integrable systems.

I do not hesitate that mathematics deserves to be cultivated for their own sake, and that the theories inapplicable to physics should be so as well as others. Even if the physical aim and the esthetic aim were not united, we ought not to sacrifice either. But more: the two aims are inseparable and the best means of attaining one is to aim at the other, or at least never to lose sight of it.
H. Poincaré