Versión itinerante a disposición de todos
La Geometría Proyectiva es toda la geometría. A. Cayley.
En el lugar de las matemáticas hay muchas moradas, y de entre ellas, la más elegante es la Geometría Proyectiva. M. Kline.
Durante el mes de Noviembre de 1999, tuvo lugar en la Facultad de Matemáticas de la Universidad Complutense de Madrid una exposición sobre la historia de la Geometría Proyectiva, desde sus orígenes en el Renacimiento, cuando los artistas comprendieron la teoría y el uso de la perspectiva, hasta finales del siglo XIX, cuando se entendió cómo la Geometría Proyectiva abarcaba a todas las demás. La exposición nació a partir de otra excelente realizada en el Instituto de Enseñanza Secundaria Miguel Servet de Madrid, titulada Arte y Geometría, y dedicada a la geometría oculta en las obras de los artistas del Renacimiento principalmente. Esta primera exposición recibió el Premio Giner de los Ríos a la Innovación Educativa, y sirvió de incentivo para la organización de la que comentamos aquí, y fue parte primordial de la misma. Los responsables de este segundo proyecto fueron María Cruz del Amo e Isabel Pinto del IES Miguel Servet de Madrid, María Emilia Alonso y Raquel Mallavibarrena del departamento de Algebra de la UCM, y Jesús M. Ruiz del departamento de Geometría y Topología de la UCM. Por supuesto, otras personas colaboraron, especialmente Pilar Vélez, del departamento de Ingeniería Industrial de la Universidad Antonio de Nebrija, e Ignacio Luengo y José Manuel Rodríguez-Sanjurjo, de los departamentos de Algebra, y de Geometría y Topología de la UCM.
Presentación y fuentes
 La exposición consistió en la exhibición permanente durante aquel mes de Noviembre de 10 paneles, que con imágenes y textos explican matemáticamente los aspectos más visuales e intuitivos de la Geometría Proyectiva. Como indica el anuncio, se organizaron a la vez tres conferencias plenarias, que impartieron Gregorio Hernández (Facultad de Informática de la Universidad Politécnica de Madrid), Luis Alvárez (departamento de Informática y Sistemas de la Universidad Politécnica de Gran Canaria) y Luis Lastra (departamento de I+D de Investrónica S.A.). Asimismo hubo varias sesiones demostrativas con ordenador, (Cabri) supervisadas y atendidas por Pilar Vélez.
La exposición consistió en la exhibición permanente durante aquel mes de Noviembre de 10 paneles, que con imágenes y textos explican matemáticamente los aspectos más visuales e intuitivos de la Geometría Proyectiva. Como indica el anuncio, se organizaron a la vez tres conferencias plenarias, que impartieron Gregorio Hernández (Facultad de Informática de la Universidad Politécnica de Madrid), Luis Alvárez (departamento de Informática y Sistemas de la Universidad Politécnica de Gran Canaria) y Luis Lastra (departamento de I+D de Investrónica S.A.). Asimismo hubo varias sesiones demostrativas con ordenador, (Cabri) supervisadas y atendidas por Pilar Vélez.
La Geometría Proyectiva tiene sus orígenes en la pintura del Renacimiento. Luego, en el siglo XVII se recuperarán ideas de los matemáticos griegos (las secciones cónicas, por ejemplo), pero son sin duda los pintores renacentistas los que fundamentan esta rama de las Matemáticas al conseguir plasmar en lienzos planos los objetos y las figuras tridimensionales tal como son, a diferencia de sus antecesores de la Edad Media. Por eso no es extraño que en esta exposición aparezcan nombres como Leonardo da Vinci, Rafael Sanzio o Alberto Durero. En el Renacimiento se investiga la visión que nuestro ojo tiene de una figura cuando la vemos en distintas pantallas colocadas entre ella y nosotros. Así nacen la perspectiva y el estudio de las proyecciones y las secciones. Son significativas las preguntas de Leone Battista Alberti en 1435: ¿Qué relación hay entre dos secciones de la misma figura?, ¿cuáles son las propiedades comunes a dos secciones cualesquiera?
Esta exposición recorre el nacimiento y la consolidación de la Geometría Proyectiva en tres fases:
1. Renacimiento: Arte y Geometría.
2. Siglo XVII: Recuperación de los conocimientos griegos y aplicaciones a la ciencia y la técnica.
3. Siglo XIX: Resurgimiento de la Geometría Pura.
Las fuentes utilizadas para la exposición han sido principalmente las siguientes:
- La geometría secreta de los pintores. C. Bouleau. Madrid: Akal 1995.
- El mundo de los grandes genios, vol. I (Leonardo da Vinci, Dalí), vol. II (Rafael). Madrid: Orbis-Fabri 1989.
- Tratado de pintura. Leonardo da Vinci. Madrid: Akal 1986.
- Piero della Francesca. M. Mangione, en Grandes Estilos de la Pintura. Pintura del Renacimiento 1. Madrid: Sedmay 1979.
- Leonardo. V. Nieto Alcaide, en Grandes Estilos de la Pintura. Pintura del Renacimiento 2. Madrid: Sedmay 1979.
- Rafael. V. Nieto Alcaide. Ibidem.
- La divina proporción. L. Pacioli. Madrid: Akal 1991.
- Van der Weyden. P. Philippot, en Grandes Estilos de la Pintura. Pintura Gótica. Madrid: Sedmay 1979.
- Leonardo da Vinci. J.Williams. Barcelona: Timun Mas 1967.
- Maestros renacentistas y barrocos del Museo Thyssen-Bornemisza. Madrid: MEC 1995.
- Plane algebraic curves. E. Brieskorn, H. Knörrer. Basilea: Birkhäuser-Verlag 1986.
- ¿Qué es la Matemática? R. Courant, H. Robbins. Madrid: Aguilar 1979.
- Projective Geometry. H.S.M. Coxeter. Berlín: Springer-Verlag 1987.
- Foundations of Projective Geometry. R. Hartshorne. Reading: Benjamin-Cummings 1967.
- The invention of infinity. J. V. Field. Oxford: Oxford Univ. Press 1997.
- Desargues en son temps. J. Dhombres, J. Sakarovitch (editores). París: Blanchard 1994.
- The geometrical work of Desargues. J.V. Field, J.J. Gray. Berlín: Springer-Verlag 1987.
- Companion Encyclopedia of the History and Philosophy of Mathematics. I. Grattan-Guinness, Londres: Routledge 1994.
- Mirar y ver. M. de Guzmán. Madrid: Alhambra 1976.
- Mathematical thought from ancient to modern times. M. Kline. Oxford: Oxford Univ. Press 1972.
- Mathematics of the 19th century. Geometry and Analytic Function Theory. A.N. Kolmogorov, A.P. Yushkevich, (editores). Basilea: Birkhäuser 1996.
- Plagiary in the Renaissance. K. Williams. Math. Intelligencer, 24, 2 (2002) 45-57.
- Imágenes de Perspectiva. J. Navarro de Zuvillaga. Madrid: Siruela 1996.
- Geometría Proyectiva. J.M. Rodríguez-Sanjurjo, J.M. Ruiz. Madrid: Addison-Wesley 1998.
- Mathematics and its History. J. Stillwell. Berlín: Springer-Verlag 1989.
- Geometría. S. Xambó. Barcelona: Ediciones UPC 1997.
- Encyclopedia Britannica.
- The MacTutor History of Mathematics Archive. Univ. St. Andrews, Escocia (http:/mathshistory.st-andrews.ac.uk/).
- Los orígenes de la Geometría Proyectiva. G. Hernández. Seminario de Historia, Facultad de Matemáticas, Madrid: UCM 1991.
- Estudio de las Geometrías. H. Eves. México: Uteha 1969.
- Euclidean and non-Euclidean Geometries, Development and History. M.J. Greenberg. Nueva York: Freeman 1993.
- Les aventures d’Anselme Lanturlu: le topologicon. J.-P. Petit. París: Belin 1985.
- Models of the real projective plane. F. Apery. Braunschweig: Vieweg-Verlag 1987.
Se dispuso un Cuaderno de Visitantes en el que se recogieron comentarios y sugerencias muy favorables a la iniciativa. Como era natural, junto al cuaderno se expuso una Superficie de Boy.

Reseña de la Gaceta de la UCM

La Facultad de Matemáticas aloja en su sótano 2, delante del salón de actos, y durante todo el mes de noviembre la exposición Origenes y nacimiento de la Geometría Proyectiva. La organización de esta iniciativa la comparten los departamentos de Algebra, y de Geometría y Topología de la Facultad y el Instituto Miguel Servet de Madrid. En la exposición se hace un recorrido histórico por la Geometría Proyectiva, desde su utilización primigenia por los artistas renacentistas como Fra Angelico, Leonardo y Uccello, hasta los modelos topológicos del plano proyectivo más modernos, como son las superficies de Steiner, la de Boy o la más popular banda de Moebius. Destaca en la exposición el análisis de cuadros renacentistas según su composición geométrica y el uso que se hizo de esta materia en ciencias como la óptica y la astronomía. El ciclo de conferencias que acompaña a la exposición se cierra el día 16 de noviembre con la ponencia Visión artificial y gráficos por ordenador impartida por Juan José Lastra. Habrá además una demostración práctica el próximo día 26 en la que se enseñará el uso del programa Cabri-Géométre con el que se verifican de manera gráfica los teoremas de geometría proyectiva.
Reportaje fotográfico de Ricardo Olmos

Vista general del acceso a los paneles

Comienzo de la exposición

Nombres propios y notas históricas

Un tratado primitivo de Perspectiva

Siempre había alguien interesado
Los paneles segundo a sexto estaban dedicados a mostrar la geometría oculta detrás de algunas de las grandes obras de los artistas renacentistas, que ellos mismos estudiaron teóricamente, como ilustran los grabados de Alberto Durero.
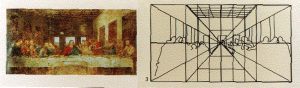
La perspectiva en La Ultima Cena de Leonardo

La geometría de la composición en El Descendimiento de van der Weyden

Otra vista general

La Madona de Port-Lligat de Dalí, que emplea a la perfección las leyes de la perspectiva

Piero, Raphael, Dalí

Más Arte y Perspectiva
A partir del sexto panel se introducían aspectos más técnicos matemáticamente.

La anamorfosis y las maquinas de ver y de dibujar.
Después se introducían las primeras nociones matemáticas rigurosas, empezando por las cónicas.

Sólo hay una cónica proyectiva, y por qué se llama cónica
Por fin, se definía el espacio proyectivo, que hay que entender añadiendo al afín los puntos de infinito.
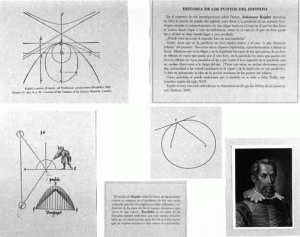
Los puntos de infinito
Mención especial aquí tenían Desargues y Pascal, autores de algunos de los más bellos teoremas clásicos de la Geometría Proyectiva, resultados que sin embargo se olvidaron durante muchos años, hasta que se produjo un redescubrimiento en el siglo XIX.
Se explicaba también la noción esencial de dualidad, crucial en la comprensión de la validez de muchos teoremas de enunciados paralelos.
Las relaciones de la geometría proyectiva con otras geometrías descubiertas a finales del siglo XIX se ilustraban con el denominado modelo proyectivo del plano hiperbólico. Asimismo se mencionaban los modelos finitos de la geometría proyectiva.
El último panel trataba de las inmersiones del plano proyectivo en el espacio afín, los modelos topológicos del plano proyectivo real.

La banda de Moebius, la superficie romana, la de Boy
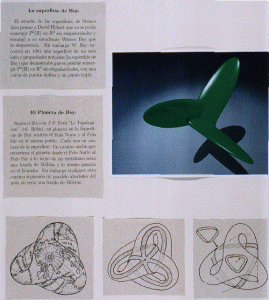
El planeta de Boy

¡No desapareció hasta el último día!
… y todo se termina.

Última foto






































