La armonía, como hemos visto anteriormente, está en el corazón mismo del pitagorismo. La música era el método de elevación y purificación del alma y al mismo tiempo objeto de contemplación intelectual que revelaba, con sus congruencias expresables mediante relaciones numéricas, la armonía más profunda del cosmos. La capacidad cuasimágica de la música es elemento heredado por el pitagorismo de las corrientes órficas más primitivas. El análisis científico de los sonidos armónicos es en cambio rasgo muy específicamente pitagórico, que casi con toda seguridad se remonta al mismo Pitágoras.Existen varias versiones sobre el modo concreto como Pitágoras llegó a desentrañar las relaciones numéricas entre los sonidos consonantes, es decir aquellos cuya producción simultánea origina una sensación agradable en nuestro oído: el tono, la octava, la quinta y la cuarta.
Nicómaco de Gerasa, Gaudencio y Boecio hablan de la observación de Pitágoras de los diferentes sonidos producidos en el yunque del herrero por martillos de diferentes pesos. Un martillo cuyo peso era como 6 producía el tono, otro con peso 12 producía la octava, otro con peso 9 la quinta y otro de peso 8 la cuarta. Pitágoras volvió a casa, colgó tales pesos de cuatro cuerdas iguales y observó que se producían los sonidos consonantes correspondientes.
Este es el ejemplo típico de una de esas historias cuya falsedad podría haber comprobado un historiador con sentido crítico sin más que tratar de repetir la experiencia. La frecuencia del sonido producido por una cuerda vibrante no está en proporción con la tensión, sino con la raíz cuadrada de la tensión.Diógenes Laercio propone a Pitágoras mismo como inventor del monocorde, no un instrumento musical, sino más bien un aparato científico para verificar la teoría musical utilizado por los pitagóricos. Gaudencio explica pormenorizadamente el experimento más verosímil con el que Pitágoras comprobó y cuantificó su intuición genial de la conexión de la armonía musical con los números. Pitágoras tensó una cuerda musical que producía un sonido que tomó como fundamental, el tono. Hizo señales en la cuerda, que la dividían en docepartes iguales. Pisó la cuerda en el 6 y entonces
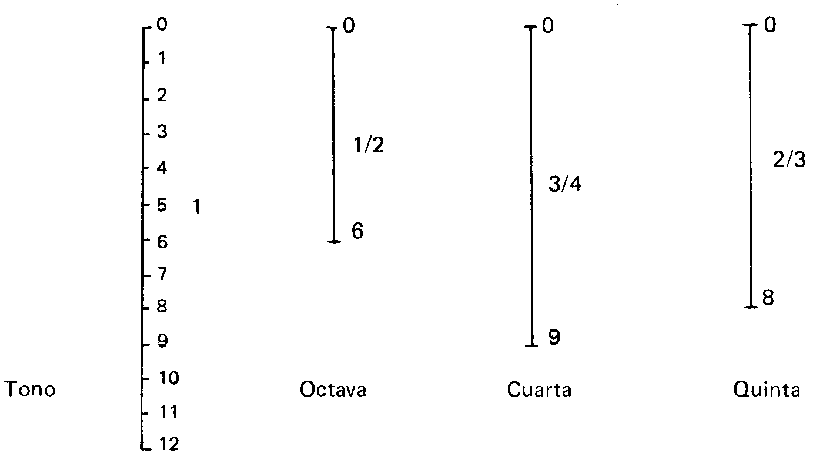
observó que se producía la octava. Pisó luego en el 9 y resultaba la cuarta. Al pisar el 8 se obtenía la quinta. ¡Las fracciones 1/2, 3/4, 2/3 correspondían a la octava, la cuarta y la quinta!. Los sonidos producidos al pisar en otros puntos resultaban discordes o al menos no tan acordes como los anteriores. ¡Los números 1,2,3,4, la Tetraktys, determinaban con sus proporciones relativas los sonidos más consonantes!.
Los números 12,9,8,6 constituyeron así mismo en el pitagorismo posterior otra cuaterna muy interesante por sus propiedades aritméticas. Se verifica:
9 = (12+6)/2
,
1/8 = 1/2 · (1/12 + 1/6)
,
12/9 = 8/6
Así 9 es media aritmética entre 12 y 6, 8 es media armónica entre 12 y 6. Se verifica 12.6=9.8 y esto es una propiedad general de la media aritmética y armónica
m = (a+b)/2
,
1/b = 1/2 · (1/a + 1/b)
luego ab = mh
Iámblico afirma que la teoría de la media aritmética y la media armónica procede de los babilonios y fue importada por Pitágoras. No hay pruebas concluyentes de tal afirmación, pero sí se puede asegurar que esta teoría pertenece al pitagorismo primitivo.
La armonía fue una ocupación constante de la escuela pitagórica en todas las etapas de su evolución.
Platón había manifestado su descontento con el carácter empírico tanto de la armonía como de la astronomía de los pitagóricos. Tal vez por su influjo se produjo una curiosa fundamentación: axiomática de la armonía pitagórica, relatada por el astrónomo Tolomeo (ca. 130 d.de C.) en su obra sobre armonía Los axiomas pueden expresarse así:
1.- A los sonidos musicales corresponden números. A los del mismo tono el mismo número, a los de distinto tono números distintos.
2.- Los números correspondientes a sonidos consonantes se comportan entre sí como el numerador y el denominador de las fracciones más perfectas a/b, que son aquéllas en que el numerador es múltiplo del denominador, a = nb, o bien aquéllas en que a sobrepasa a b en una parte de b, es decir a=b+b/n, y esta relación es tanto más perfecta cuanto más simple, es decir cuanto más pequeño sea n.
3.- A la octava, como más perfecta, debe corresponder la relación 2/1.
De esta forma resulta por pura deducción lógica que a la quinta le debe corresponder 3/2 y a la cuarta 4/3.
De entre los desarrollos ulteriores de la armonía científica de los pitagóricos se puede destacar la explicación, asombrosamente acertada, de la naturaleza del sonido como una sucesión de percusiones en el aire, haciendo depender el tono del número de percusiones que se producen por unidad de tiempo, es decir, de la frecuencia. Con ello se explica de modo natural y exacto la producción de sonidos fisiológica y psicológicamente agradables, consonantes, en la cuerdas cuyas longitudes se comportan como los números más sencillos. Las percusiones del aire producidas simultáneamente por una cuerda y la cuerda con la misma tensión, de longitud mitad, tono y octava, llegan al tímpano de una forma representable en el eje del tiempo de la manera siguiente:

Su composición da lugar a una estructura de percusiones como la que sigue:

que es sencilla y previsible, armoniosa, para nuestro oído.
En cambio la producción de dos sonidos de frecuencias de percusión arbitrarias dará lugar a una estructura un tanto caótica que para nuestro oído resulta opaca, no previsible, en una palabra, disonante. Para mayor información sobre estos problemas profundamente interesantes puede consultarse el artículo de B.L. van de Waerden, Die Harmonielehre der Pythagoreer, Hermes 78 (1943) 163.

