CÓNICAS. PRECEDENTES: MEMECMO, ARISTEO, EUCLIDES, ARQUÍMEDES…
El trabajo más importante de Apolonio se refiere a las secciones cónicas. La cuestión previa interesante que en este apartado examinaremos es la siguiente: ¿qué se sabía sobre cónicas antes de Apolonio?.
Debido precisamente a la perfección de la obra de Apolonio, los tratados que sobre cónicas fueron escritos antes que el de Apolonio no han sido conservados. Se conocen noticias aisladas que se pueden encontrar en los escritores que describen el desarrollo de la geometría.
Menecmo, hacia 350 a.de C., se ocupa del problema clásico de la duplicación del cubo (construir un cubo de doble volumen que otro dado), en cuya motivación y descripción no entraremos aquí. Redujo el problema al de la construcción de las dos medias proporcionales entre 2 y 1. En nuestro lenguaje, si encontramos x e y tales que
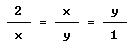
entonces
x2=2y, y2=x
y así
x3=2y3
es decir, el cubo de lado x es de volumen doble que el de lado y. En general, el problema de las dos medias proporcionales entre a y b consiste en hallar x e y, tales que
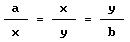
Su resolución se reduce a hallar la intersección de la curva x2=ay con xy=ab y es así como aparecen lo que nosotros llamamos parábola e hipérbola equilátera.
Menecmo introduce estas curvas como secciones de un cono circular recto por un plano perpendicular a una generatriz. Por eso la parábola fue llamada, y con esta terminología aparece todavía en Arquímedes, sección de cono rectángulo (es decir sección de cono cuyo ángulo de apertura es recto por un plano perpendicular a una generatriz). La elipse era la sección de cono acutángulo y la hipérbola (hasta Apolonio solo se consideró una rama de ella) la sección de cono obtusángulo.
El desarrollo de la teoría de cónicas debió de ser muy rápido pues ya hacia fines del siglo IV existieron dos obras importantes. La primera es de Aristeo, el Libro de los lugares sólidos (lugares planos eran los que dan lugar a rectas y círculos; lugares sólidos son aquéllos en los que aparecen las cónicas por intersección de cilindros y conos con planos; lugares lineales eran otras curvas de orden superior no reducibles a las anteriores como la cuadratrix o la concoide). La segunda obra de interés, también perdida, fue de euclides, en cuatro libros, cuyo contenido debió de ser en sus líneas fundamentales el que se encuentra en los cuatro primeros libros de las Cónicas de Apolonio, si bien menos general y menos sistemático.
De este modo, al final del siglo IV, ya eran bien conocidas propiedades tales como la de la ordenada
![]()
Y también la de las asíntotas de la hipérbola
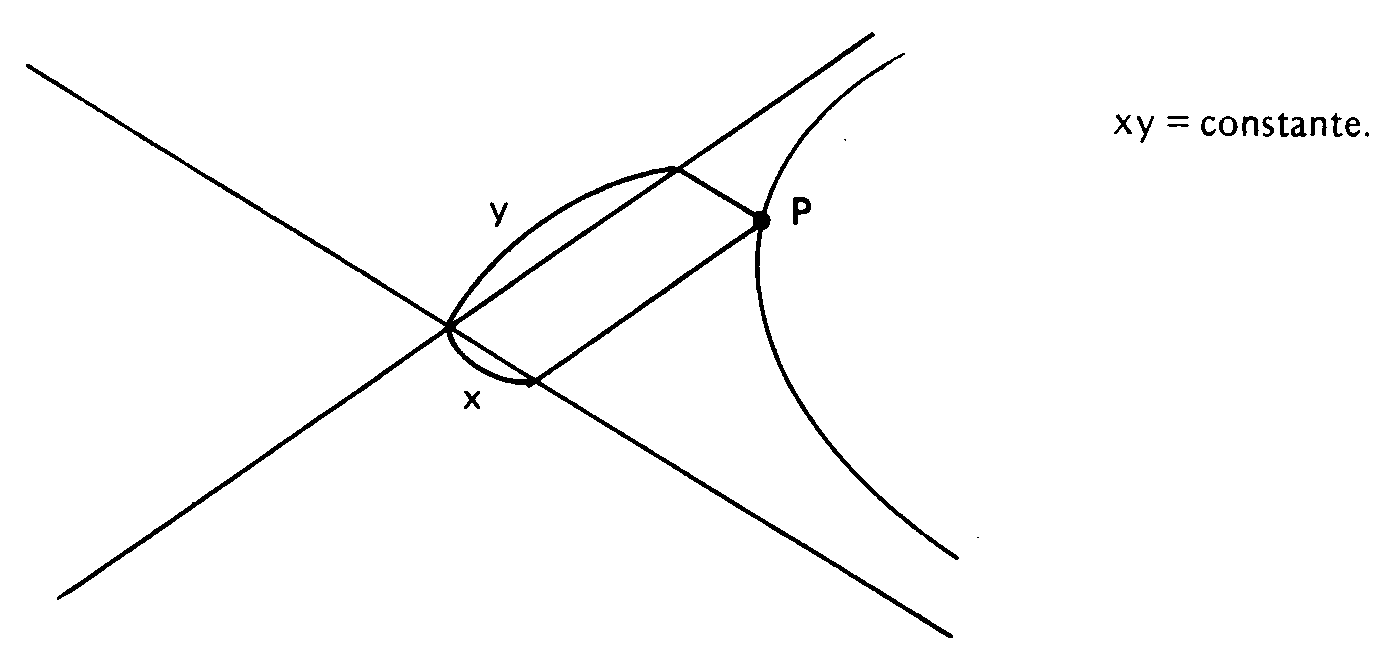
He aquí el modo sencillo como Menecmo pudo llegar a la propiedad que hoy expresamos y2=2px para la sección del cono rectángulo (parábola)
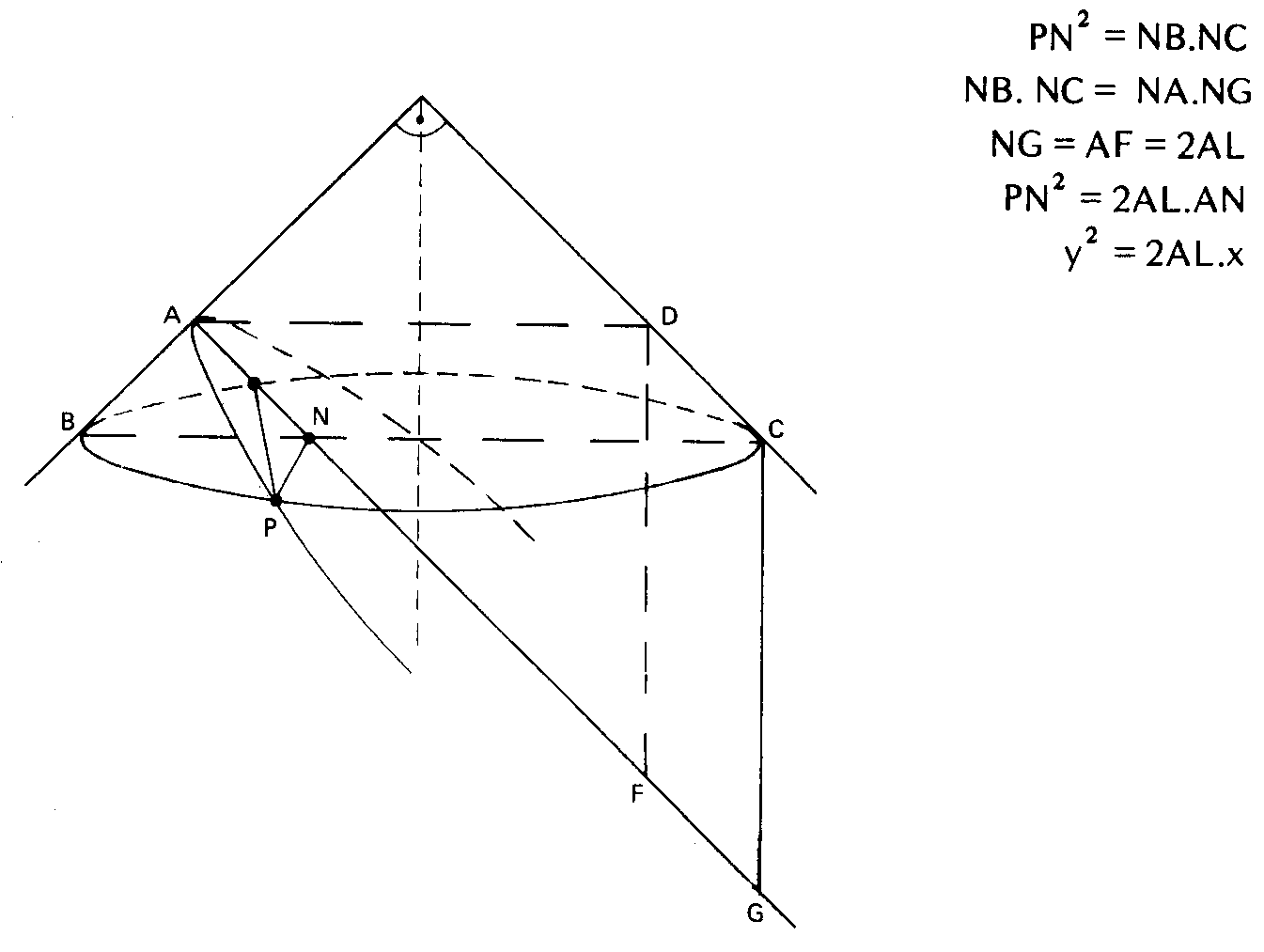
Arquímedes se especializó en propiedades de la parábola. Muchas de las que cita en sus obras las propone como del dominio público en su tiempo. Así la de la subnormal y el hecho de que si PV es un diámetro que biseca la cuerda QQ´ y si la tangente en Q interseca el diámetro en T entonces
PV=PT

