LA ARITMÉTICA DE LOS PITAGÓRICOS.

Al estudiar la aritmética de los pitagóricos es necesario distinguir claramente entre la aritmética científica y la aritmética popular. La aritmética científica de los griegos se encuentra resumida en los libros VII, VIII y IX de los Elementos de Euclides que fueron escritos hacia el año 300 a. de C. Por testimonios históricos se puede concluir que algunas porciones de los libros VII y VIII es obra de los pitagóricos. En particular el libro VII debe de proceder de los matemáticos anónimos anteriores a Arquitas y el VIII de los de la escuela de Arquitas. Algunas porciones del libro IX, como la doctrina del «par e impar» es anterior incluso a los pitagóricos anónimos y posiblemente procede del tiempo de Hipaso de Metaponto (hacia el año 500 a. de C.).     No me ocuparé aquí de detallar específicamente el contenido de esta aritmética científica, pues esto será realizado en otra conferencia de esta serie, por el profesor Alberto Dou, dedicada a Euclides. Sólo quisiera señalar dos puntos particularmente notables de la aritmética de los Elementos, de los cuales uno con seguridad es de procedencia pitagórica y el otro con gran probabilidad también.

El primero se refiere a los llamados «números lado y diagonal». El segundo es el llamado «algoritmo de Euclides» para la obtención del máximo común divisor de dos números. Los números lado y diagonal constituyen pares de números formados recursivamente que servían a los pitagóricos para aproximar mediante fracciones, cada vez con mayor exactitud, la relación entre la diagonal y el cuadrado, es decir para aproximar la raíz de 2. De esta forma se expresa Proclo en su comentario al libro sobre la República de Platón:
«La unidad, como origen de todos los números, es potencialmente tanto lado como diagonal. Se toman ahora dos unidades: una como unidad-lado y otra como unidad-diagonal y se forma un nuevo lado, añadiendo a la unidad-lado la unidad-diagonal, y una nueva diagonal, añadiendo a la unidad-diagonal el doble de la unidad-lado»

El proceso de formación de los pares de números lado y diagonal prosigue de la misma forma. El nuevo lado es suma de los números lado y diagonal anteriores, la nueva diagonal es la suma de la diagonal anterior y dos veces el lado anterior, es decir:

 

 

¿De dónde proviene la extraña idea de este proceso recursivo, probablemente el primero de tal naturaleza en la historia de la matemática?.

Según Proclo, los pitagóricos demostraron el siguiente teorema:

» Si L y D son lado y diagonal de un cuadrado, entonces también  L* =L+D y D*=D+2L son lado y diagonal de un cuadrado»

Y Proclo afirma que la demostración de los pitagóricos de esta propiedad se realizó mediante la proposición II, 10 de los Elementos de Euclides, que representa la identidad que nosotros escribiríamos así

(2X+Y)²+Y²=2X²+2(X+Y)²

En efecto, si suponemos que X=L, Y=D son lado y diagonal de un cuadrado, se tiene D²=2L² y así substituyendo arriba y simplificando Y²=2X², resulta

(2L+D)²=2(L+D)²

es decir, 2L+D es diagonal del cuadrado de lado L+D.

Es posible que la idea original de tal hilo de pensamiento y de demostración esté implicita en el proceso de antanairesis con el que, según O.Becker y otros (Cf. O.Becker, Grösse und Grenze der Mathematischen Denkweise, Karl Alber Verlag, 1959; trad. esp. Rialp, 1969) se procedía originariamente a la demostración de la irracionalidad de raíz de 2. El proceso aparece muy claramente sugerido por la siguiente figura:

 

 

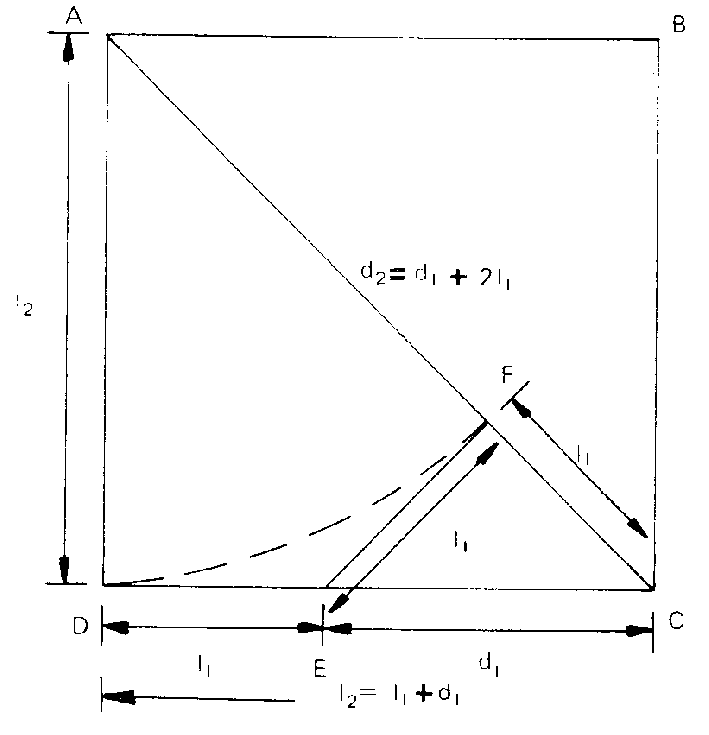
Si l₁=EF y d₁=EC son lado y diagonal de un cuadrado, entonces DC=l₂=l₁+d1 y AC=d₂=d₁+2l₁ son también lado y diagonal de otro cuadrado. El proceso de antanairesis es efectivamente la vuelta atrás del proceso de construcción de los pares de números lado y diagonal. En realidad, desde el punto de vista matemático es mucho más razonable pensar que el camino de las ideas fue el inverso, es decir, a fin de hallar la unidad común, si existe, capaz de medir al tiempo lado l₂ y diagonal d₂, era natural substraer de la diagonal el lado l₂, obteniendo así CF y luego tratar de hallar la unidad común de CF=l₁ y DC=d₂, restando CF=EF=DE de DC para obtener así EC=d₁. Al tratar de obtener la unidad común de EC=d₁ y FC=l₁ observamos que estamos en las condiciones iniciales pues d₁ y l₁ son diagonal y lado de un nuevo cuadrado. El proceso no acaba nunca y esto viene a demostrar la no existencia de tal unidad común. La vuelta atrás de esta antanairesis aplicada al cuadrado fue probablemente la motivación del método de construcción de los números lado y diagonal.

El proceso de antanairesis que hemos seguido no es otra cosa que la versión geométrica del algoritmo de Euclides para la obtención del máximo común divisor de dos números (VII, 33). Así, tanto por la estructura lógica de los libros VII y VIII de los Elementos como por consideraciones históricas, parece razonable concluir que los pitagóricos, en particular probablemente alguno de los matemáticos anónimos del siglo V conoció y estructuró estos dos algoritmos de una brillantez y profundidad que aún hoy día nos llenan de asombro.

La aritmética popular de los pitagóricos tenía otro sabor totalmente distinto del de estos retazos de la aritmética científica que hemos examinado. Su finalidad era hacer inteligible a todos las fascinantes propiedades de los números. La principal fuente de nuestro conocimiento de esta aritmética es la Introducción a la Aritmética de Nicómaco de Gerasa (ca. 50-150 d. de C.), obra que se extendió extraordinariamente a juzgar por el gran número de manuscritos (44) que de ella se conservan. En este trabajo aparecen por extenso la teoría figurativa de los números, los números triangulares, cuadrados rectangulares, pentagonales, etc. y se habla de las fabulosas y místicas propiedades de ciertos números en concreto.