LA COMUNIDAD PITAGÓRICA. GENERACIONES DE MATEMÁTICOS.
Los ciudadanos de Crotona propusieron, al parecer, a Pitágoras que continuase su labor de formación moral e intelectual de jóvenes y adultos. Los esfuerzos de Pitágoras se debieron de centrar, en lo que concierne a la formación personal completa, en los jóvenes a quienes encontró más flexibles y con más capacidad de absorber el espíritu pitagórico plenamente. Puesto que su sistema de pensamiento estaba basado en el descubrimiento y contemplación de la armonía del cosmos y a ello se habría de llegar muy fundamentalmente a través de la introducción en consideraciones científicas, muy difíciles para los más adultos, ocupados en los asuntos de la ciudad, estableció de modo natural dos formas distintas de enseñanza. Así es como explica Iámblico (Vita Pyth. 88) la existencia en la primitiva comunidad pitagórica de dos clases de miembros, los matemáticos (mathematikoi, conocedores) es decir los iniciados a quienes Pitágoras comunicaba los conocimientos científicos a su disposición y los acusmáticos (akousmatikoi, oidores) que participaban de los conocimientos y creencias, de los principios morales, ritos y prescripciones específicas de la hermandad, si bien sin conocer en profundidad las razones de su credo y su proceder. Esta distinción resultó ser de enorme trascendencia en la evolución de la comunidad pitagórica. Los acusmáticos se constituyeron en custodios de las enseñanzas de Pitágoras y su preocupación fue que éstas se conservaran tal como Pitágoras las había transmitido. Los matemáticos se consideraban continuadores más bien del espíritu de Pitágoras, basado en el conocimiento científico, y puesto que es connatural a éste su propia evolución era claro para ellos que el conjunto de conocimientos de Pitágoras era susceptible de perfeccionamiento. Era natural que esta diversidad de pareceres había de conducir a la división de la comunidad con la desaparición de Pitágoras y así sucedió en efecto.
La distinción entre matemáticos y acusmáticos es transmitida por múltiples canales. Iámblico es quien narra más por extenso la división entre ellos y su narración parece haber sido tomada de la obra perdida de Aristóteles sobre los pitagóricos. Al parecer fue Hipaso el principal representante de los matemáticos. Se debió de ocupar con notable éxito de hacer avanzar los conocimientos matemáticos. A principios del siglo V (500-480) entró en conflicto con los acusmáticos, ya que fue el primero en ofrecer por escrito al público en general «el secreto de la esfera de los doce pentágonos» (Iámblico, Vita Pyth.88), en castigo de lo cual murió en un naufragio. El «secreto de la esfaera de los doce pentágonos» alude a cierta construcción relacionada con el dodecaedro regular que los pitagóricos primitivos deseaban mantener en secreto, como el grueso de su doctrina en general. En otro lugar Iámblico mismo (Vita Pyth. 246-247) cuenta que aquél que reveló «la naturaleza del conmensurable y del inconmensurable a quienes no eran dignos de participar de tales conocimientos», fue expulsado de la comunidad. Los pitagóricos le erigieron una tumba como si para ellos ya hubiera muerto. Parece probable que fue Hipaso mismo este personaje que reveló por primera vez la existencia de longitudes inconmensurables y precisamente a través de un estudio del pentágono regular como veremos más adelante. Iámblico acusa a Hipaso de haberse atribuído el mérito de sus descubrimientos, «siendo así que todos proceden de El», es decir de Pitágoras. Se puede pensar razonablemente que Hipaso fue un gran matemático que efectivamente dió por primera vez con la existencia de longitudes inconmensurables, es decir tales que una no es un múltiplo de una parte de la otra, dando con ello al traste con la acariciada creencia de los pitagóricos primitivos de que todo debe estar regido por los números enteros y las proporciones entre ellos. La versión que Iámblico cuenta, acusando a Hipaso de plagio, proviene según la conjetura de van der Waerden, del círculo de pitagóricos matemáticos anónimos entre 480-430 de quienes la tomó Aristóteles mismo. Estos pitagóricos fueron potentes matemáticos con la estrategia común de atribuir a Pitágoras mismo sus descubrimientos matemáticos.
¿Como pudo tener lugar el descubrimiento de Hipaso de los inconmensurables?. En 1954 Kurt von Fritz publicó un artículo importante, The Discovery of Incommensurability by Hippasus of Metapontum, Annals of Mathematics 46 (1954), 242-264. De acuerdo con sus investigaciones se puede pensar que fue más o menos como sigue. Los pitagóricos primitivos estaban profundamente familiarizados con el pentágono regular. Según parece el emblema que les servía para reconocimiento mutuo era el pentagrama, es decir la estrella de cinco puntas formada por las diagonales de un pentágono regular. En sus cinco vértices solían colocar las letras de la palabra ugieia, salud. Las razones de la especial veneración de los pitagóricos por esta figura no nos es bien conocida, pero uno se inclina a pensar que en ella, al igual que en la tetraktis, que luego examinaremos más a fondo, encontraban armonías geométricas y numéricas extraordinariamente llamativas. Es fácil ver que todos los ángulos que aparecen en la figura son múltiplos enteros del más pequeño de entre ellos (72º=2×36º, 108º=3×36º, 144º=4×36º, 180º=5×36º). Parece natural que los pitagóricos se preguntaran sobre la proporción en que se encuentran también los segmentos que aparecen en esta figura.
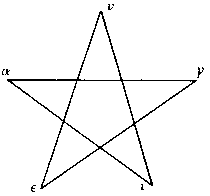
No es difícil ver, siempre con los elementos que los pitagóricos del tiempo de Hipaso tenían a su disposición, que cada segmento de los dibujados está con el que es inmediatamente mayor exactamente en la misma proporción, que es precisamente la proporción los pitagóricos tenían ya, como veremos más tarde en detalle, el proceso denominado antanairesis, o cancelación de uno y otro lado, que se corresponde geométricamente con el llamado algoritmo de Euclides para hallar el máximo común divisor de dos números.
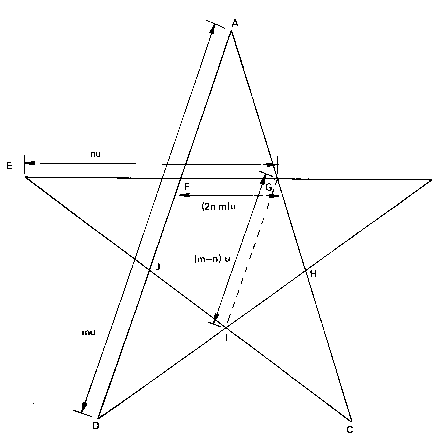
Suppongamos que los segmento señalados en la figura por AD y EG son conmensurables es decir que existe un segmento u tal que AD mide mu y EG mide nu. Tratamos de determinar la fracción m/n. Podemos suponer que m/n está en forma irreducible, es decir, suponemos que no existen números naturales, m* menor que m, y n* menor que n, tales que m/n=m*/n*. De la figura misma es sencillo deducir que GI mide (m-n)u y que GF mide (2n-m)u. Por otra parte es claro que AD y GI son diagonales de pentágonos regulares de lados EA= EG y GF respectivamente. Por tanto AD/EG=GI/GF, es decir m/n=(m-n)/(2n-m). LLamando m*= m-n, n*=2n-m, hemos obtenido una contradicción con nuestra hipótesis de que m/n era fracción irreducible. Así nuestro punto de partida de que AD y EG son conmensurables es falso.
Así como entre los pitagóricos acusmáticos, como es natural, apenas se pueden distinguir etapas evolutivas, entre los pitagóricos matemáticos que se dedicaron al desarrollo de la ciencia estas etapas se pueden diferenciar con cierta probabilidad. Así van der Waerden distingue cinco generaciones en el pitagorismo entre los años 530-360.
1ª Generación (530-500): Pitágoras.
2ª Generación (520-480): Hipaso de Metaponto, Alcmeon.
3ª Generación (480-430): Matemáticos anónimos.
4ª Generación (440-400): Filolao, Teodoro.
5ª Generación (400-360): Arquitas de Tarento.
Los matemáticos anónimos de la tercera generación debieron de constituir un grupo muy interesante del que Aristóteles se hace eco con admiración. De ellos habla como de los fundadores de la matemática tal como se cultivaba en su tiempo, una matemática bien adulta, rigurosa y ampliamente evolucionada. De ellos decía Aristóteles(según Iámblico De communi math. sci. 78) que «estiman mucho la exactitud de la argumentación en las ciencias matemáticas, porque solo ellas poseen demostraciones». Más adelante tendremos ocasión de examinar el fuerte impacto que dejaron en la geometría y en la aritmética, que quedó plasmado en los Elementos de Euclides.
Filolao, de la 4ª generación, fue de estilo grandilocuente y ampuloso, sin mucho rigor matemático. Su astronomía también carece de rigor científico. Conocía y utilizaba los conocimientos matemáticos, pero su lógica y su matemática resulta más bien floja.

