EL PAIS, miércoles 16 de diciembre de 1992
FUTURO/3
La muerte de una neurona de Bourbaki
Jean Dieudonné fue el alma del célebre colectivo científico que llenó de «matemática moderna» las escuelas.
MIGUEL DE GUZMÁN
Washington University, Saint Louis, Misuri (EEUU). Primavera de 1968. Cena en casa de 1os Boothby. El profesor Boothby, un experto geómetra, ha pasado el semestre anterior en el Politécnico de Zúrich (Suiza). La señora Boothby ha aprovechado la estancia allí para seguir un curso de cocina francesa. Esa cena es como la defensa de su tesis doctoral. Desde el primer plato yo 1e daría sobresaliente cum laude sin dificultad. Pero el presidente del tribunal es Jean Dieudonné, experto cocinero, gourmet y catador de vinos capaz de adivinar 1a cosecha por el olor del sacacorchos incluso antes de descorchar la botella.
La señora Boothby se va ganando a pulso su notable mientras que entre copa y copa Dieudonné nos cuenta los recuerdos de la formación matemática que se estilaba en París durante su juventud… «Para ingreso en las grandes escuelas el eje de nuestra preparación consistía en tratar de derrotar a enemigo». El enemigo no era, como podría uno pensar ingenuamente, el problema matemático propuesto, sino el compañero de banco. Era necesario demostrar que valías más que él. Esta concepción pugilística de 1a matemática había resultado muy influyente en su carrera. Desde aquella cena creo haber podido entender un poco mejor la personalidad de Dieudonné, uno de los matemáticos más influyentes de los últimos 50 años, que ha muerto hace pocos días en París a los 86 años.
Su valía como matemático de primera categoría en áreas muy diversas, incluida la historia de la matemática, es proclamada bien alto por todos los especialistas, así como la profundidad de su influencia. Sus méritos han sido ampliamente reconocidos con multitud de distinciones de Gobiernos y centros académicos de todo el mundo. La Real Academia de Ciencias española contaba a Dieudonné entre sus miembros correspondientes desde 1970.
En esta breve nota quisiera resaltar su participación en uno de los episodios más interesantes de la historia de las matemáticas en nuestro siglo, el fenómeno Bourbaki. Como Bourbaki nunca nació, tampoco puede morir propiamente, pero bien merece que se le dedique un recuerdo con ocasión de la muerte de Dieudonné.
Seudónimo
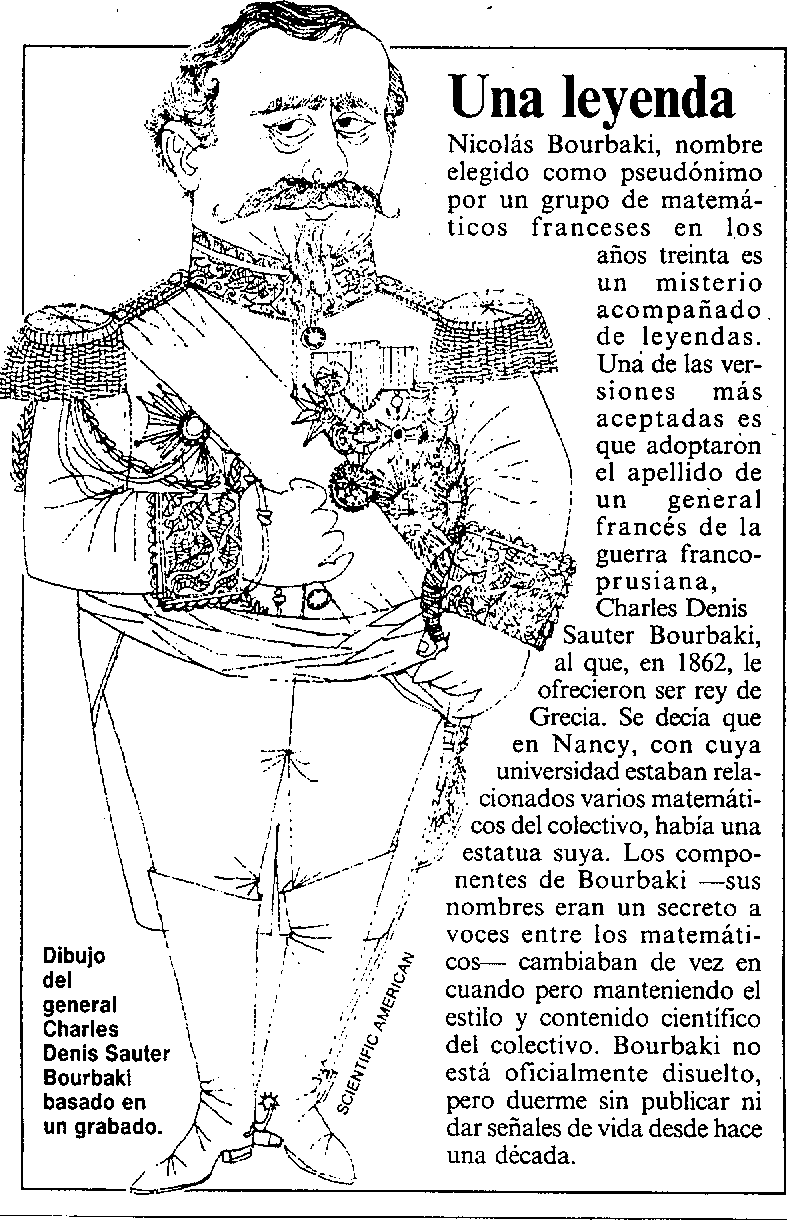
Dieudonné fue una de las neuronas más activas en el cerebro de Bourbaki, y su personalidad asoma a menudo en las afirmaciones tajantes y avasalladoras de esta figura mítica. Nicolás Bourbaki fue el seudónimo colectivo (si bien Bourbaki escribe siempre en singular) de un fuerte grupo de matemáticos, casi todos franceses, y algunos de ellos, entre los cuales se contó Dieudonné, de excepcional valor. Se propusieron hacia los años treinta ir desarrollando todo el edificio de la matemática a partir de sus elementos fundamentales.

«Afirmo que sobre estos fundamentos puedo construir el cuerpo entero de las matemáticas de hoy y que si hay algo original en mis procedimientos eso consiste solamente en el hecho de que, en lugar de contentarme con tal afirmación, procedo a demostrarla del mismo modo que Diógenes demostró la existencia del movimiento, y mi demostración llegará a ser más y más completa a medida que mi tratado vaya creciendo». El tratado creció y creció a partir de 1939 con el nombre de Éléments de mathématique (Hermann et Cie., París) y su influencia se hizo notar cada vez más intensamente en líneas muy diversas de la actividad matemática.
Empresa ambiciosa
El intento inicial de ofrecer unos «fundamentos de la matemática, para el matemático», como una especie de compilación básica, sistemática y ordenada de los conocimientos matemáticos del tiempo, fue una empresa extraordinariamente ambiciosa.
En el siglo III antes de Cristo, Euclides pudo llevar a cabo con éxito una tarea semejante. Sus Elementos resultaron ser un texto de trabajo en que se educaron los matemáticos de 22 siglos. Pero tratar de hacer algo semejante en el siglo XX con la aparición constante de nuevos campos y teorías motivadas por intereses siempre cambiantes y apoyadas en innovaciones tecnológicas profundas, hubiera podido parecer una misión imposible para cualquier humano.
No para Dieudonné, que fue desde el principio la cabeza más o menos invisible de una especie de corporación de entre 10 y 20 jóvenes investigadores matemáticos que tomaron sobre sus hombros la tarea de escribir los Elementos de la matemática para el siglo XX.
La obra Éléments de mathématique, en infinidad de tomos, tuvo un éxito que debió de sorprender al mismísimo Nicolás Bourbaki. Pero su influjo, visto ahora con cierta perspectiva, no ha resultado en su conjunto muy positivo, aunque es posible que Nicolás Bourbaki no tuviera toda la culpa. El aspecto más pernicioso de su influencia ha sido el estilo bourbakista de abordar la matemática que en los años cincuenta y sesenta fue constituyendo una moda dictatorial en muchos ámbitos diferentes de la investigación y de la exposición matemática en los textos y en la enseñanza. Hubo muchos que interpretaron mal la intención de Bourbaki.
La forma bourbakista de exposición, el formalismo que sólo se permite en sus procedimientos partir de axiomas bien explícitamente establecidos, sin apelar en ningún momento a los contenidos intuitivos y prácticos que dan su motivación a las construcciones matemáticas, era considerado el único modo admisible para la exposición matemática y, lo que ha sido más dañino, para la enseñanza misma a todos los niveles, incluida la enseñanza secundaria, y aún en muchos casos, la primaria.
Geometría desterrada
En los centros universitarios de numerosos países donde la actividad matemática era entonces fundamentalmente pasiva y receptiva, incluído el nuestro, buena parte de la enseñanza en aquellos años tenía como base los tratados de Bourbaki y toda ella estaba embebida en la moda formalista que Bourbaki había impuesto. La enseñanza secundaria y primaria fue invadida por la corriente llamada «matemática moderna», con su proliferación de la teoría de conjuntos y con el destierro de la geometría de corte más clásico, sustituida por nociones bastante inoperantes y aburridas de álgebra abstracta.
La educación matemática se va recuperando poco a poco y con gran esfuerzo de tales tendencias, que los años han revelado inoperantes. La moraleja de tales consideraciones podría ser la siguiente: si mentes tan claras como la de Dieudonné y otros bourbakistas son capaces de empujar a la comunidad matemática por caminos que hoy generalmente se reconocen como claramente equivocados, parece que hay que pensar que los problemas de la educación en un tema tan lleno de implicaciones para el desarrollo científico y tecnológico de un país han de ser tratados con sumo cuidado.
Miguel de Guzmán es catedrático de análisis matemático de la Universidad Complutense de Madrid y presidente de la Comisión Internacional de Educación Matemática.

