Las Cónicas de Apolonio.
Las circunstancias de la composición de la obra de Apolonio están explicadas por él mismo en su primer libro. Así le escribe a Eudemo: «Creo que no habrás olvidado, porque ya te lo he contado antes, que fue a instancias de Naucrates el geómetra, que fue mi huésped durante su estancia en Alejandría, por lo que me introduje en este campo y que, cuando él estaba a punto de embarcarse, me apresuré a ponerle al corriente de lo que había ya elaborado, en ocho libros, sin poner demasiado cuidado en su perfección, sino anotando todo lo que se me ocurría, con la intención de hacer una ulterior revisión. Ahora que he tenido la ocasión de establecer las cosas por sus pasos de una manera adecuada, las publico. Y puesto que sucede que algunos de los que han tratado conmigo han recibido los libros primero y segundo antes de que hubiesen sido revisados, no te extrañes de encontrar en ellos cuestiones tratadas de una manera diferente…».
Apolonio sabe mucho más de lo que hasta entonces se sabía y de modo mucho mejor organizado. Por ello se decide a publicarlo. El mismo, en este prólogo al libro primero, explica el contenido de la obra bien claramente. Los cuatro primeros libros constituyen una introducción elemental. Debían de constituir materia probablemente ya sabida, pero no organizada como la propone Apolonio. A partir del libro V se exponen los hallazgos más importantes del mismo Apolonio.
Su indice, con palabras nuestras, se puede proponer más o menos así:
I. Modos de obtención y propiedades fundamentales de las cónicas.
II. Diámetros, ejes y asíntotas.
III. Teoremas notables y nuevos. Propiedades de los focos.
IV. Número de puntos de intersección de cónicas.
…………………………………………………………………………………………………………………………………
V. Segmentos de máxima y mínima distancia a las cónicas. Normal, evouta, centro de curvatura.
VI. Igualdad y semejanza de las secciones cónicas. Problema inverso: dada la cónica, hallar el cono.
VII. Relaciones métricas sobre diámetros.
VIII. (Se desconoce su contenido. Tal vez problemas sobre diámetros conjugados).
A continuación examinaremos someramente algunos de los detalles más importantes de los diferentes libros, adelantando solamente que se considera, de modo unánime, el libro V como el mejor y más original de todos.
El libro I comienza con la generación del cono circular oblicuo de dos hojas que, seccionado por un plano, dará lugar a los diferentes tipos de cónicas. Apolonio ha captado cómo esta consideración de un solo cono permite la obtención de las tres cónicas según la inclinación diversa del plano y además identificará la hipérbola como una curva con dos ramas. En estos puntos importantes se aparta de sus antecesores en el campo, logrando una visión más unitaria y mejor sistematizada del tema.
Estudia las secciones circulares del cono, paralelas y antiparalelas a la base, introduce el parámetro (p=2b2/a) que llama lado recto, establece las propiedades de ordenada y abscisa de las cónicas, considera el centro, ejes, diámetros conjugados, tangentes, … y ataca el problema de construcción de la cónica dados diversos elementos suyos.
El libro II estudia fundamentalmente las propiedades de las asíntotas de la hipérbola. Caracteriza la asíntota por la distancia PM en función de OP y el parámetro correspondiente (ver figura).
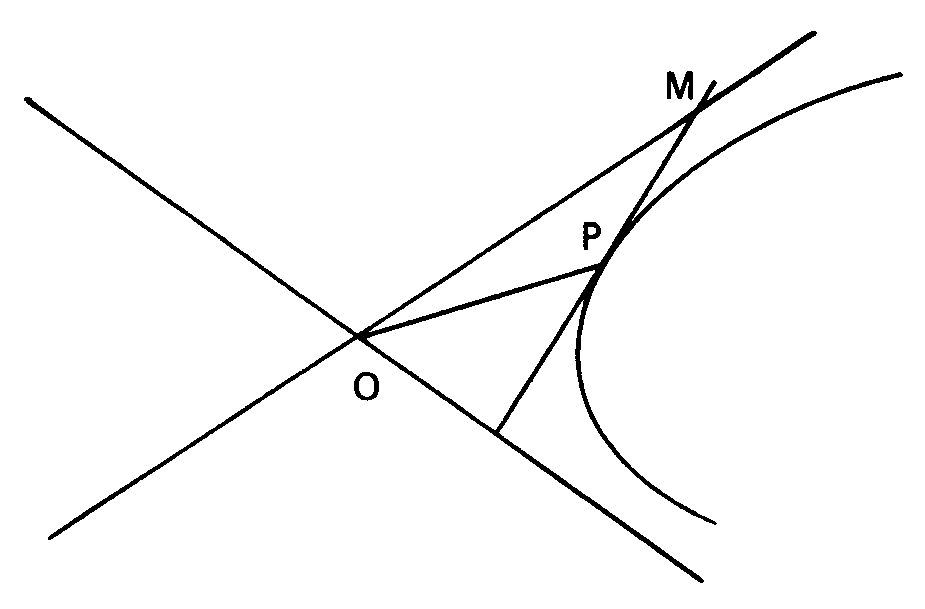
Estudia al final el problema importante siguiente: Trazar una tangente que forme un ángulo dado con el diámetro que pasa por el punto de contacto.
El lenguaje de Apolonio es, por supuesto, un lenguaje sintético, utilizando a la perfección los viejos procedimientos pitagóricos de la aplicación de áreas. Los resultados sin embargo son fácilmente traducibles al lenguaje de la geometría analítica. Lo que resulta profundamente sorprendente y llamativo es que Apolonio sea capaz de llegar tan lejos sin asomo de utilización de los métodos avanzados de la geometría y del cálculo de los que nosotros disponemos.
El libro III se dedica primero a estudiar las relaciones de triángulos y cuadriláteros determinados por tangentes y diámetros conjugados. Obtiene la relación armónica sobre los cuatro puntos determinados en una secante a la cónica que pasa por un punto, su polar y los dos de intersección de la secante con la cónica. En la proposición 41 se establece cómo tres tangentes a la parábola se cortan en la misma razón y así resulta la parábola como envolvente de las rectas con esta propiedad. En la proposición 43 aparece la hipérbola como lugar de puntos tales que xy=constante, siendo x e y abscisa y ordenada respecto a los ejes constituídos por las asíntotas. Desde la proposición 45 a la 52 aparecen propiedades interesantes sobre los focos. En la 45 se establece cómo desde un foco F se ve bajo un ángulo recto MFM´ el segmento determinado por una tangente cualquiera entre las tangentes en A y A´ (ver figura).
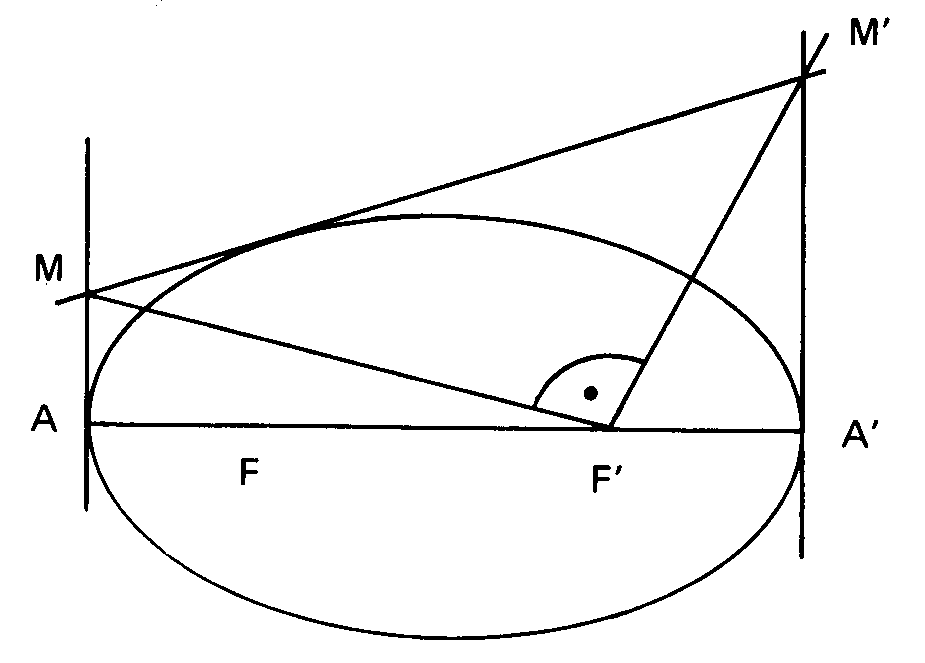
La proposición 49 afirma esencialmente que la podaria del foco es el círculo de diámetro AA´ en la elipse e hipérbola. La 52 contiene lo que hoy solemos tomar a veces como definición de elipse (PF+PF´=2a).
Los focos, en Apolonio, son ta ek ehs parabolhs geuhqeuta ohmeia es decir, «los puntos que surgen de la aplicación» de áreas.
El libro IV es de bastante menos valor. En él estudia el número de puntos de intersección de las cónicas. Es interesante desde un punto de vista lógico que de sus 57 proposiciones, las 23 primeras se demuestran por reducción al absurdo.
El libro V, que consta de 77 proposiciones es, con gran diferencia, el más sorprendente de todos. Se puede decir que en él Apolonio, 20 siglos antes que Huygens (en su Horologium Oscillatorium, 1673) introduce ya, a su modo, con instrumentos puramente sintéticos, nociones tales como normal a una curva, evoluta, centro de curvatura, etc,.. y que logra obtener estos elementos para las cónicas de la manera más rigurosa.
Es interesante observar cómo Apolonio explicita en el prólogo al libro V la novedad de sus consideraciones: «En este libro quinto he expuesto proposiciones relativas a los segmentos de máxima y mínima distancia. Has de saber que mis predecesores y contemporáneos solo superficialmente han tratado la investigación de las líneas de distancia mínima y solamente han probado qué líneas rectas tocan a las secciones cónicas y qué propiedades tienen en virtud de ser tangentes. Por mi parte yo he probado estas propiedades en el libro primero (sin hacer uso sin embargo en las demostraciones de la teoría de las líneas de distancia mínima).…..Las proposiciones en las que trato los segmentos de distancia mínima las he separado en clases y he tratado cada una con una demostración cuidadosa. También he puesto en conexión estas cuestiones con las relativas a los segmentos de distancia máxima que antes he mencionado, porque consideraba que los que cultivan esta ciencia las necesitan a fin de obtener un conocimiento del análisis y discusión (determinación de los límites de posibilidad, dwrismoi ) de los problemas así como de su síntesis. Por otra parte, esta materia es una de esas que parecen dignas de estudio por sí mismas».
La normal desde un punto exterior viene definida a través de la propiedad de máxima o mínima distancia desde el punto a la curva. Apolonio comienza por considerar el punto E sobre el eje principal tal que AE=p/2.
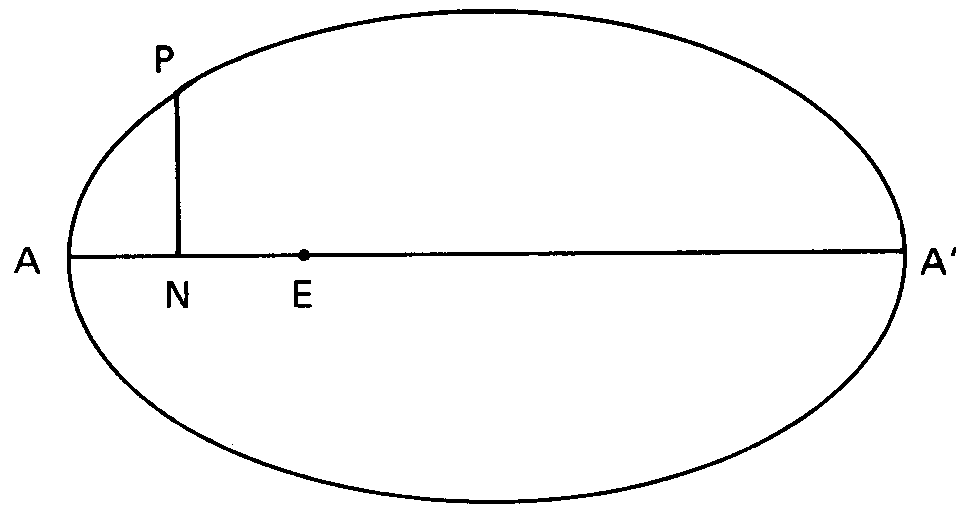
Demuestra entonces que para cualquier punto P sobre la elipse se verifica PE2=AE2+AN2((AA´+p)/AA´) y así está a distancia de E mayor que A. Por tanto AE es para E el segmento de distancia mínima desde E a la elipse. Considera luego E en situaciones más generales y análogamente determina la normal desde E. Las proposiciones más llamativas de toda la obra son ciertamente la 51 y 52 de este libro quinto. En ellas consigue ¡por procedimientos puramente sintéticos! obtener la evoluta de las cónicas como lugar de los centros de curvatura, mediante la determinación del número de normales distintas desde cada punto. Esto equivale a describir sintéticamente las curvas que en el lenguaje de nuestra geometría analítica tendrían por ecuación
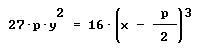
(parábola)
(ax)2/3 + (by)2/3 = (a2 + b2)2/3
(elipse, hipérbola)
En las proposiciones 55-63 obtiene las normales desde un punto exterior reduciendo el problema a la determinación del pie de la normal sobre la cónica por intersección de ésta con una hipérbola equilátera asociada al punto exterior.
En el libro VI, dedicado fundamentalmente a la igualdad y semejanza de cónicas aparece el problema interesante siguiente: dada la cónica y dado un cono circular recto hallar una sección del cono que sea igual a la cónica dad. Es llamativa la elegancia de la resolución de este problema.
Las proposiciones del libro VII, nuevas en su mayor parte, como Apolonio mismo señala, contienen numerosas relaciones métricas entre diámetros conjugados, áreas, etc…

